题目内容
如图,在四棱锥 中,底面
中,底面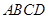 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面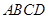 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.

(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
 中,底面
中,底面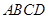 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面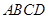 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;(2)求三棱锥
 的体积.
的体积.(1)见解析(2)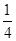
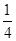
试题分析:(1)由题意知四边形BCDE为平行四边形,故连结CE交BD于O,知O是EC的中点,又M是PC的中点,根据中位线定理知MO∥PE,根据线面平行判定定理可得PE∥面BDM;(2)三棱锥P-MBD就是三棱锥P-BCD割去一个三棱锥M-BCD,故三棱锥P-MBD体积就是三棱锥P-BCD体积减去一个三棱锥M-BCD的体积,由PA=PD=AD=2及
 为
为 的中点知,PE垂直AD,由面面垂直的性质定理知PE⊥面ABCD,故PE是三棱锥P-BCD的高,由M是PC的中点知三棱锥M-BCD的高为PE的一半,故三棱锥P-MBD体积为三棱锥P-BCD体积的一半,易求出三棱锥P-BCD即可求出三棱锥P-MBD体积.
的中点知,PE垂直AD,由面面垂直的性质定理知PE⊥面ABCD,故PE是三棱锥P-BCD的高,由M是PC的中点知三棱锥M-BCD的高为PE的一半,故三棱锥P-MBD体积为三棱锥P-BCD体积的一半,易求出三棱锥P-BCD即可求出三棱锥P-MBD体积.试题解析:
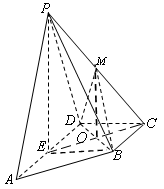
(1)连接
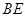 ,因为
,因为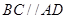 ,
,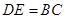 ,所以四边形
,所以四边形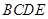 为平行四边形,
为平行四边形,连接
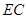 交
交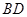 于
于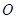 ,连接
,连接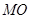 ,则
,则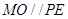 ,
,又
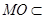 平面
平面 ,
,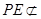 平面
平面 ,所以
,所以 平面
平面 .
.(2)
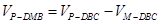 ,
,由于平面
 底面
底面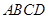 ,
,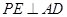
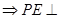 底面
底面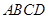
所以
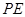 是三棱锥
是三棱锥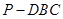 的高,且
的高,且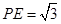
由(1)知
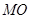 是三棱锥
是三棱锥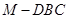 的高,
的高,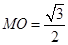 ,
,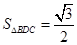 ,
,所以
 ,则
,则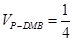 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过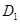 、E、F作平面
、E、F作平面 交
交 于G.
于G. ;
; 的余弦值;
的余弦值; 的体积.
的体积.


 中侧棱垂直于底面,
中侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱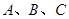 三点在球心为
三点在球心为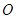 的球面上,
的球面上,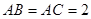 ,
,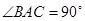 ,球心
,球心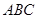 的距离为
的距离为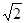 ,则球
,则球 中,
中,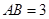 ,
, ,
, ,若把
,若把 旋转一周,则所形成的几何体的体积是( )
旋转一周,则所形成的几何体的体积是( )




 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
 A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P
A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P