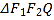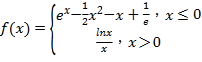题目内容
【题目】点
为坐标原点，直线
经过抛物线
的焦点
.
（1）若点到直线的距离为
， 求直线的方程；
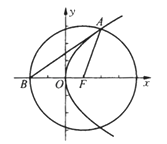
（2）设点
是直线与抛物线
在第一象限的交点.点
是以点为圆心，
为半径的圆与
轴负半轴的交点.试判断直线
与抛物线的位置关系，并给出证明.
【答案】（1）
；（2）直线
与抛物线相切，证明见解析.
【解析】
（1）抛物线的焦点
，当直线
的斜率不存在时，即
不符合题意．当直线的斜率存在时，设直线的方程为：
，所以
，由此能求出直线的方程．
（2）直线与抛物线相切．设
，
，则
．因为
，所以
，
，由此能够证明直线与抛物线相切．
解：（1）抛物线的焦点
，
当直线的斜率不存在时，即不符合题意.
当直线的斜率存在时，
设直线的方程为：
，即
.
所以，，解得：
.
故直线的方程为：
，即
（2）直线与抛物线相切，证明如下：
设
，则.
因为，所以
.
所以直线的方程为：
，
整理得：
（1）
把方程（1）代入
得：
，
，
所以直线与抛物线相切.
阅读快车系列答案【题目】通过随机询问
名不同性别的大学生是否爱好某项运动，得到如下的
列联表：
男 | 女 | |
爱好 | 40 | 20 |
不爱好 | 20 | 30 |
由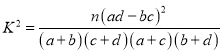
算得
，
参照附表，以下不正确的有（ ）
附表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过
的前提下，认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过的前提下，认为“爱好该项运动与性别无关”
C.有
以上的把握认为“爱好该项运动与性别有关”
D.有以上的把握认为“爱好该项运动与性别无关”
【题目】某社区消费者协会为了解本社区居民网购消费情况，随机抽取了100位居民作为样本，就最近一年来网购消费金额(单位：千元)，网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间
内，按
，
，
，
，
，
分成6组，其频率分布直方图如图所示.
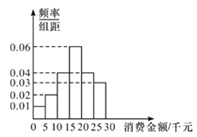
（1）估计该社区居民最近一年来网购消费金额的中位数；
（2）将网购消费金额在20千元以上者称为“网购迷”，补全下面的
列联表，并判断有多大把握认为“网购迷与性别有关系”；
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
（3）调査显示，甲、乙两人每次网购采用的支付方式相互独立，两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式，所得数据如下表所示：
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率，若甲、乙两人在下周内各自网购2次，记两人采用支付宝支付的次数之和为
，求的数学期望.
附：观测值公式：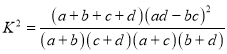
临界值表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
