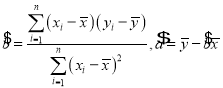题目内容
【题目】在平面直角坐标系中,设点![]() ,定义
,定义![]() ,其中
,其中![]() 为坐标原点,对于下列结论:
为坐标原点,对于下列结论:
![]() 符合
符合![]() 的点
的点![]() 的轨迹围成的图形面积为8;
的轨迹围成的图形面积为8;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则
上任意一点,则![]() ;
;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则使得“
上任意一点,则使得“![]() 最小的点
最小的点![]() 有无数个”的必要条件是
有无数个”的必要条件是![]() ;
;
![]() 设点
设点![]() 是圆
是圆![]() 上任意一点,则
上任意一点,则![]() .
.
其中正确的结论序号为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
![]() 根据新定义由
根据新定义由![]() ,讨论x的取值,得到y与x的分段函数关系式,画出分段函数的图象,由图象可知点P的轨迹围成的图形为边长是
,讨论x的取值,得到y与x的分段函数关系式,画出分段函数的图象,由图象可知点P的轨迹围成的图形为边长是![]() 的正方形,求出正方形的面积即可;
的正方形,求出正方形的面积即可;
![]() 运用绝对值的含义和一次函数的单调性,可得
运用绝对值的含义和一次函数的单调性,可得![]() 的最小值;
的最小值;
![]() 根据
根据![]() 大于等于
大于等于![]() 或
或![]() ,把
,把![]() 代入即可得到当
代入即可得到当![]() 最小的点P有无数个时,k等于1或
最小的点P有无数个时,k等于1或![]() ;而k等于1或
;而k等于1或![]() 推出
推出![]() 最小的点P有无数个,得到
最小的点P有无数个,得到![]() 是“使
是“使![]() 最小的点P有无数个”的充要条件;
最小的点P有无数个”的充要条件;
![]() 把P的坐标用参数表示,然后利用三角函数的化积求得
把P的坐标用参数表示,然后利用三角函数的化积求得![]() 的最大值说明命题正确.
的最大值说明命题正确.
![]() 由
由![]() ,根据新定义得:
,根据新定义得:![]() ,
,
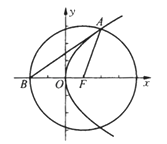
由方程表示的图形关于x,y轴对称和原点对称,
且![]() ,
,
画出图象如图所示:

根据图形得到:四边形ABCD为边长是![]() 的正方形,面积等于8,
的正方形,面积等于8,
故![]() 正确;
正确;
![]() 为直线:
为直线:![]() 上任一点,可得
上任一点,可得![]() ,
,
可得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,可得
时,可得![]() ,综上可得
,综上可得![]() 的最小值为1,故
的最小值为1,故![]() 正确;
正确;
![]() ,当
,当![]() 时,
时,![]() ,满足题意;
,满足题意;
而![]() ,当
,当![]() 时,
时,![]() ,满足题意.
,满足题意.
![]() “使
“使![]() 最小的点P有无数个”的充要条件是“
最小的点P有无数个”的充要条件是“![]() ”,
”,![]() 正确;
正确;
![]() 点P是圆
点P是圆![]() 上任意一点,则可设
上任意一点,则可设![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 正确.
正确.
则正确的结论有:![]() 、
、![]() 、
、![]() .
.
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2019年春节档有多部优秀电影上映,其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况,得到如下表格:
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况,试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率;
(2)以表中各评价等级对应的频率作为各评价等级对应的概率,假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名,求恰有2名评价为五星1名评价为一星的概率;
(ii)若从全国所有观众中随机选取16名,记评价为五星的人数为X,求X的方差.
【题目】为了解某地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(已知:![]() 则认为
则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般,
线性相关性一般,![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y与x的线性回归方程,并预测该地区2019年足球特色学校的个数(精确到个位)
参考公式:
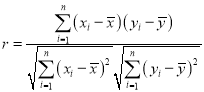
![]() ;
;