题目内容
12.设Sn为数列{an}的前n项和,且对?n∈N*,点(an,Sn)都在函数f(x)=-$\frac{1}{2}$x+$\frac{1}{2}$的图象上,等差数列{bn}的首项b1=1,公差d>0,且b2,b5,b14成等比数列.(1)求数列{an}与{bn}的通项公式
(2)若数列{cn}对?n∈N*,都有$\frac{{C}_{1}}{{a}_{1}}$+$\frac{{C}_{2}}{{a}_{2}}$+…+$\frac{{C}_{n}}{{a}_{n}}$=bn+1成立,求数列{cn•bn}的前n项和Tn.
分析 (1)通过将点(an,Sn)代入函数f(x)=-$\frac{1}{2}$x+$\frac{1}{2}$,利用an=Sn-Sn-1及${S}_{1}=-\frac{1}{2}{a}_{1}+\frac{1}{2}$计算即得an=$(\frac{1}{3})^{n}$;利用b2=1+d,b5=1+4d,b14=1+13d及b2,b5,b14成等比数列,计算即得bn=2n-1;
(2)通过$\frac{{c}_{1}}{{a}_{1}}$+$\frac{{c}_{2}}{{a}_{2}}$+…+$\frac{{c}_{n}}{{a}_{n}}$=bn+1与$\frac{{c}_{1}}{{a}_{1}}$+$\frac{{c}_{2}}{{a}_{2}}$+…+$\frac{{c}_{n}}{{a}_{n}}$+$\frac{{c}_{n+1}}{{a}_{n+1}}$=bn+2作差,计算可得数列{cn}的通项,利用Tn与$\frac{1}{3}$Tn相减,计算即得结论.
解答 解:(1)∵点(an,Sn)都在函数f(x)=-$\frac{1}{2}$x+$\frac{1}{2}$的图象上,
∴Sn=-$\frac{1}{2}$an+$\frac{1}{2}$,Sn-1=-$\frac{1}{2}$an-1$+\frac{1}{2}$(n≥2),
∴an=Sn-Sn-1=(-$\frac{1}{2}$an+$\frac{1}{2}$)-(-$\frac{1}{2}$an-1$+\frac{1}{2}$)=$\frac{1}{2}$an-1-$\frac{1}{2}$an,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{1}{3}$,
又${S}_{1}=-\frac{1}{2}{a}_{1}+\frac{1}{2}$,∴a1=$\frac{1}{3}$,
∴an=$(\frac{1}{3})^{n}$;
∵等差数列{bn}的首项b1=1,公差d>0,
∴b2=1+d,b5=1+4d,b14=1+13d,
又∵b2,b5,b14成等比数列,
∴(1+4d)2=(1+d)(1+13d),
整理得:d=2或d=0(舍),
∴bn=1+2(n-1)=2n-1;
(2)∵$\frac{{c}_{1}}{{a}_{1}}$+$\frac{{c}_{2}}{{a}_{2}}$+…+$\frac{{c}_{n}}{{a}_{n}}$=bn+1,
∴$\frac{{c}_{1}}{{a}_{1}}$+$\frac{{c}_{2}}{{a}_{2}}$+…+$\frac{{c}_{n}}{{a}_{n}}$+$\frac{{c}_{n+1}}{{a}_{n+1}}$=bn+2,
∴$\frac{{c}_{n+1}}{{a}_{n+1}}$=bn+2-bn+1=2,
∴cn+1=2an+1=2•$(\frac{1}{3})^{n+1}$,
又$\frac{{c}_{1}}{{a}_{1}}$=b2,∴c1=a1•b2=1,
∴数列{cn}的通项cn=$\left\{\begin{array}{l}{1,}&{n=1}\\{2•(\frac{1}{3})^{n},}&{n≥2}\end{array}\right.$,
∴Tn=1×1+3×2×$(\frac{1}{3})^{2}$+5×2×$(\frac{1}{3})^{3}$+7×2×$(\frac{1}{3})^{4}$+…+(2n-1)×2×$(\frac{1}{3})^{n}$,
∴$\frac{1}{3}$Tn=1×1×$\frac{1}{3}$+3×2×$(\frac{1}{3})^{3}$+5×2×$(\frac{1}{3})^{4}$+…+(2n-3)×2×$(\frac{1}{3})^{n}$+(2n-1)×2×$(\frac{1}{3})^{n+1}$,
两式相减得:$\frac{2}{3}$Tn=1+$\frac{2}{3}$-$\frac{1}{3}$+4[$(\frac{1}{3})^{3}$+$(\frac{1}{3})^{4}$+…+$(\frac{1}{3})^{n}$]-(2n-1)×2×$(\frac{1}{3})^{n+1}$
=$\frac{4}{3}$+4×$\frac{(\frac{1}{3})^{3}[1-(\frac{1}{3})^{n-2}]}{1-\frac{1}{3}}$-(2n-1)×2×$(\frac{1}{3})^{n+1}$
=$\frac{14}{9}$-$\frac{4(n+1)}{3}$•$\frac{1}{{3}^{n}}$,
∴Tn=$\frac{7}{3}$-2(n+1)•$\frac{1}{{3}^{n}}$.
点评 本题考查了等差数列与等比数列的通项公式、递推式的应用,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
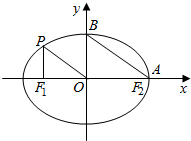 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |