题目内容
8.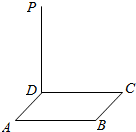 已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8
已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8(Ⅰ)连接PB、AC,证明:PB⊥AC;
(Ⅱ)连接PA,求PA与平面PBD所成的角的正弦值.
分析 (Ⅰ)欲证PB⊥AC,只需证明AC垂直PB所在平面即可,因为PB在平面PBD中,AC垂直平面PBD中的两条相交直线PD和BD,所以问题得证.
(Ⅱ)欲求PA与平面PBD所成的角的大小,只需找到PA在平面PBD中的射影,PA与它的射影所成角即为所求,再放入三角形中,解三角形即可.
解答 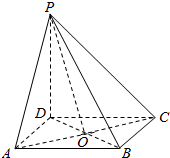 (Ⅰ)证明:连接BD,在正方形ABCD中,AC⊥BD,
(Ⅰ)证明:连接BD,在正方形ABCD中,AC⊥BD,
又PD⊥平面ABCD,所以,PD⊥AC,
所以AC⊥平面PBD,故PB⊥AC.
(Ⅱ)解:因为AC⊥平面PBD,设AC与BD交于O,连接PO,则∠APO就是PA与平面PBD所成的角,
在△APO中,AO=3$\sqrt{2}$,AP=10,
所以sin∠APO=$\frac{3\sqrt{2}}{10}$,
所以∠APO=arcsin$\frac{3\sqrt{2}}{10}$,
所以PA与平面PBD所成的角的大小为arcsin$\frac{3\sqrt{2}}{10}$.
点评 本题主要考查了直线与直线垂直的证明,直线与平面所成角的计算,以及点到平面的距离的求法,属于立体几何的常规题.

练习册系列答案
相关题目
18.将分别写有A,B,C,D,E,F的6张卡片装入3个不同的信封里中.若每个信封装2张,其中写有A,B的卡片装入同一信封,则不同的方法共有( )
| A. | 12种 | B. | 18种 | C. | 36种 | D. | 54种 |
16.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{asin2x,0≤x≤π}\end{array}\right.$.若方程f(x)=1有3个不同的实数根,则实数a的取值范围是( )
| A. | (1,+∞) | B. | {-1}∪(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
20.观察下列各式:
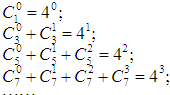
照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )
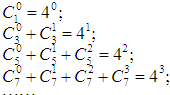
照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )
| A. | 4n+1 | B. | 4n | C. | 4n-1 | D. | 4n-2 |
14.已知数列{an}的前n项和Sn=n2-2n,则 a2+a10=( )
| A. | 20 | B. | 19 | C. | 18 | D. | 17 |