题目内容
16.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{asin2x,0≤x≤π}\end{array}\right.$.若方程f(x)=1有3个不同的实数根,则实数a的取值范围是( )| A. | (1,+∞) | B. | {-1}∪(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
分析 当x<0时,由f(x)=x2=1得x=-1;从而可得,当0≤x≤π时,方程sin2x=$\frac{1}{a}$有2个不同的解;作函数y=sin2x,(0≤x≤π)的图象,结合图象求解即可.
解答 解:当x<0时,f(x)=x2=1,解得,x=-1;
∵方程f(x)=1有3个不同的实数根,
∴当0≤x≤π时,方程f(x)=1可化为asin2x=1;
显然可知a=0时方程无解;
故方程可化为sin2x=$\frac{1}{a}$,且有2个不同的解;
作函数y=sin2x,(0≤x≤π)的图象如下,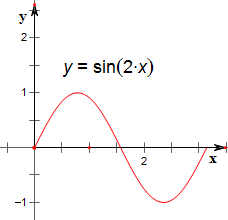
结合图象可得,
0<$\frac{1}{a}$<1或-1<$\frac{1}{a}$<0;
解得,a∈(-∞,-1)∪(1,+∞);
故选D.
点评 本题考查了分段函数的应用及方程的根与函数的图象的交点的应用,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
4.函数f(x)=x3+3x2+3x-a的极值点的个数是( )
| A. | 2 | B. | 1 | C. | 0 | D. | 由a确定 |
2.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.独立性检验观察值计算公式$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,独立性检验临界值表:
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.独立性检验观察值计算公式$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,独立性检验临界值表:
| P(K2≥k0) | 0.50 | 0.25 | 0.15 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 0.455 | 1.323 | 2.072 | 3.841 | 5.024 | 6.635 | 7.879 |
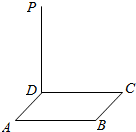 已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8
已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8