题目内容
3.已知直线l∥平面α,l的一个方向向量为(t,2,4),α的法向量为($\frac{1}{2}$,1,2),则实数t的值为-20.分析 利用线面平行与垂直的性质、向量垂直与数量积的关系即可得出.
解答 解:∵直线l∥平面α,l的一个方向向量为$\overrightarrow{u}$=(t,2,4),α的法向量为$\overrightarrow{v}$=($\frac{1}{2}$,1,2),
∴$\overrightarrow{u}•\overrightarrow{v}$=$\frac{1}{2}t+2+8$=0,
解得t=-20.
故答案为:-20.
点评 本题考查了线面平行与垂直的性质、向量垂直与数量积的关系,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.已知数列{an}、{bn}、{cn}的通项公式分别为:an=n,bn=n(n+1),cn=n(n+1)(n+2),数列{an},{bn}的前n项和分别为S1(n),S2(n),观察下表:
发现S1(n)=$\frac{1}{2}$bn,并可用下面方法证明:
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| an | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| S1(n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | … |
| bn | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | … |
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
 已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8
已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8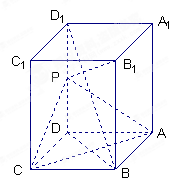 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.