题目内容
9.已知函数f(x)的定义域为(-1,1),对于任意的x,y∈(-1,1),有f(x)+f(y)=f($\frac{x+y}{1+xy}$),且当-1<x<0时,f(x)>0.(1)求f(0)的值,并判断函数f(x)的奇偶性;
(2)若f($\frac{a+b}{1+ab}$)=1,f($\frac{a-b}{1-ab}$)=2,且|a|<1,|b|<1,求f(a),f(b)的值;
(3)若f(-$\frac{4}{5}$)=1,求f(x)在[-$\frac{1}{2}$,$\frac{1}{2}}$]上的值域.
分析 解:(1)令x=y=0可得f(0)+f(0)=f(0),从而解得f(0)=0;再令y=-x∈(-1,1)即可;
(2)由题意得$\left\{\begin{array}{l}f(a)+f(b)=1\\ f(a)+f(-b)=1\end{array}\right.$,从而可得$\left\{\begin{array}{l}f(a)+f(b)=1\\ f(a)-f(b)=1\end{array}\right.$;从而解得;
(3)可得$f(\frac{4}{5})=-1$,从而可得$f({\frac{1}{2}})=-\frac{1}{2}$;由定义法可判断f(x)在区间(-1,1)内为减函数;从而求值域即可.
解答 解:(1)∵$f(x)+f(y)=f(\frac{x+y}{1+xy})$①,
∴由①式令x=y=0,得f(0)+f(0)=f(0),
∴f(0)=0;
由①式令y=-x∈(-1,1),得f(x)+f(-x)=f(0);
∴函数f(x)是奇函数.
(2)由①式及已知,得$\left\{\begin{array}{l}{f(a)+f(b)=1}\\{f(a)+f(-b)=2}\end{array}\right.$,
由(1)知函数f(x)是奇函数,
∴$\left\{\begin{array}{l}{f(a)+f(b)=1}\\{f(a)-f(b)=2}\end{array}\right.$;
解得$f(a)=\frac{3}{2},f(b)=-\frac{1}{2}$.
(3)∵$f(-\frac{4}{5})=1$,
∴$f(\frac{4}{5})=-1$.
又∵$f({\frac{1}{2}})+f({\frac{1}{2}})=f({\frac{4}{5}})$,
∴$f({\frac{1}{2}})=-\frac{1}{2}$;
设-1<x1<x2<1,
∴x1-x2<0,1-x1x2>0,∴$\frac{{{x_1}-{x_2}}}{{1-{x_1}{x_2}}}<0$.
又由题设知,当-1<x<0时,f(x)>0.
则$f({x_1})-f({x_2})=f({x_1})+f(-{x_2})=f(\frac{{{x_1}-{x_2}}}{{1-{x_1}{x_2})}})>0$,
∴f(x1)>f(-x2),
∴f(x)在区间(-1,1)内为减函数;
于是有$f({\frac{1}{2}})≤f(x)≤f({-\frac{1}{2}})$.
f(x)在$[{-\frac{1}{2},\frac{1}{2}}]$上的值域为$[{-\frac{1}{2},\frac{1}{2}}]$.
点评 本题考查抽象函数的应用及函数的性质的判断与应用,属于中档题.

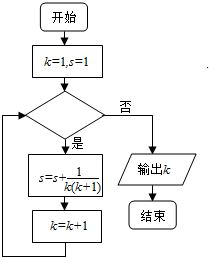
| A. | k<2012 | B. | k<2013 | C. | k<2014 | D. | k<2015 |
| A. | y=3x-1 | B. | y=-3x-1 | C. | y=3x+1 | D. | y=-2x-1 |
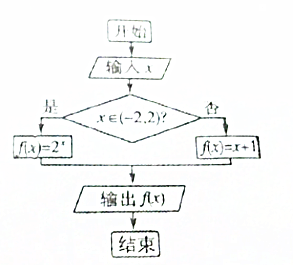 阅读如图的程序框图,若输出的函数值f(x)为4,则输入的自变量x的值为3.
阅读如图的程序框图,若输出的函数值f(x)为4,则输入的自变量x的值为3.