题目内容
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2(n=1,2,…),a1=1.
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)设cn=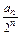 (n=1,2,…),求证:数列{cn}是等差数列;
(n=1,2,…),求证:数列{cn}是等差数列;
(3)求数列{an}的通项公式及前n项和公式.
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)设cn=
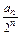 (n=1,2,…),求证:数列{cn}是等差数列;
(n=1,2,…),求证:数列{cn}是等差数列;(3)求数列{an}的通项公式及前n项和公式.
(1)证明略(2)证明略(3){an}的前n项和公式为Sn=(3n-4)·2n-1+2
(1)证明 ∵Sn+1=4an+2,
∴Sn+2=4an+1+2,两式相减,得
Sn+2-Sn+1=4an+1-4an(n=1,2,…),
即an+2=4an+1-4an,
变形得an+2-2an+1=2(an+1-2an)
∵bn=an+1-2an(n=1,2,…),∴bn+1=2bn.
由此可知,数列{bn}是公比为2的等比数列.
(2)证明 由S2=a1+a2=4a1+2,a1=1.
得a2=5,b1=a2-2a1=3.故bn=3·2n-1.
∵cn=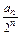 (n=1,2,…),
(n=1,2,…),
∴cn+1-cn= -
-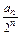 =
= =
= .
.
将bn=3·2n-1代入得
cn+1-cn= (n=1,2,…),
(n=1,2,…),
由此可知,数列{cn}是公差为 的等差数列,
的等差数列,
它的首项c1= =
= ,故cn=
,故cn= n-
n- (n=1,2,…).
(n=1,2,…).
(3)解 ∵cn= n-
n- =
= (3n-1).
(3n-1).
∴an=2n·cn=(3n-1)·2n-2 (n=1,2,…)
当n≥2时,Sn=4an-1+2=(3n-4)·2n-1+2.
由于S1=a1=1也适合于此公式,
所以{an}的前n项和公式为Sn=(3n-4)·2n-1+2.
∴Sn+2=4an+1+2,两式相减,得
Sn+2-Sn+1=4an+1-4an(n=1,2,…),
即an+2=4an+1-4an,
变形得an+2-2an+1=2(an+1-2an)
∵bn=an+1-2an(n=1,2,…),∴bn+1=2bn.
由此可知,数列{bn}是公比为2的等比数列.
(2)证明 由S2=a1+a2=4a1+2,a1=1.
得a2=5,b1=a2-2a1=3.故bn=3·2n-1.
∵cn=
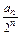 (n=1,2,…),
(n=1,2,…),∴cn+1-cn=
 -
-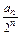 =
= =
= .
.将bn=3·2n-1代入得
cn+1-cn=
 (n=1,2,…),
(n=1,2,…),由此可知,数列{cn}是公差为
 的等差数列,
的等差数列,它的首项c1=
 =
= ,故cn=
,故cn= n-
n- (n=1,2,…).
(n=1,2,…).(3)解 ∵cn=
 n-
n- =
= (3n-1).
(3n-1).∴an=2n·cn=(3n-1)·2n-2 (n=1,2,…)
当n≥2时,Sn=4an-1+2=(3n-4)·2n-1+2.
由于S1=a1=1也适合于此公式,
所以{an}的前n项和公式为Sn=(3n-4)·2n-1+2.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 .
. ;
; 为
为 的一个极值点,证明
的一个极值点,证明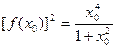 .
.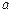 与
与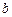 不共面,直线
不共面,直线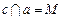 ,直线
,直线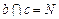 ,又
,又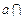 平面
平面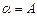 ,
,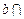 平面
平面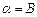 ,
,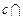 平面
平面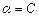 ,求证:
,求证: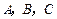 三点不共线.
三点不共线.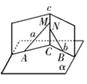
 中,若
中,若 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想 ,那么
,那么 ”时,假设的内容应是
”时,假设的内容应是

 ,用
,用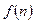 表示线段
表示线段 上除端点外的所有整点(坐标是整数的点)的个数,则
上除端点外的所有整点(坐标是整数的点)的个数,则 的值是( )
的值是( )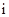 是虚数单位,若复数
是虚数单位,若复数 是纯虚数,则实数
是纯虚数,则实数 等于
等于 .
.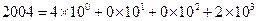 ,那么在5进制中数码2004折合成十进制为
,那么在5进制中数码2004折合成十进制为