题目内容
如图所示,已知直线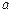 与
与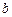 不共面,直线
不共面,直线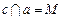 ,直线
,直线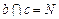 ,又
,又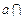 平面
平面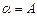 ,
,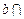 平面
平面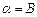 ,
,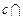 平面
平面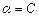 ,求证:
,求证: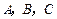 三点不共线.
三点不共线.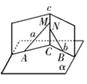
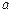 与
与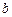 不共面,直线
不共面,直线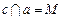 ,直线
,直线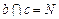 ,又
,又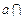 平面
平面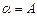 ,
,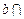 平面
平面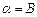 ,
,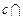 平面
平面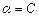 ,求证:
,求证: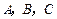 三点不共线.
三点不共线.
证明见解析
证明:用反证法,假设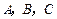 三点共线于直线
三点共线于直线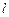 ,
,
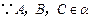 ,
,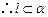 .
.
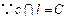 ,
,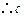 与
与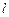 可确定一个平面
可确定一个平面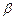 .
.
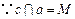 ,
,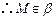 .
.
又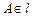 ,
,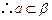 ,同理
,同理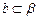 ,
,
 直线
直线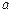 ,
,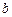 共面,与
共面,与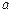 ,
,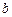 不共面矛盾.
不共面矛盾.
所以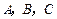 三点不共线.
三点不共线.
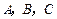 三点共线于直线
三点共线于直线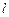 ,
,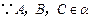 ,
,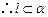 .
.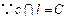 ,
,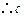 与
与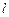 可确定一个平面
可确定一个平面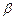 .
.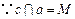 ,
,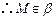 .
.又
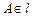 ,
,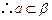 ,同理
,同理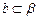 ,
, 直线
直线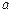 ,
,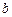 共面,与
共面,与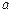 ,
,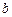 不共面矛盾.
不共面矛盾.所以
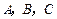 三点不共线.
三点不共线.
练习册系列答案
相关题目
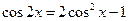 (
(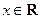 )的两边求导,得:
)的两边求导,得: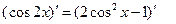 ,
,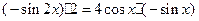 ,化简得等式:
,化简得等式: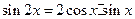 。
。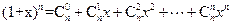 (
(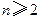 ),证明:
),证明: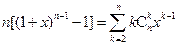 。
。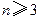 ,求证:
,求证: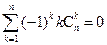 ; (ii)
; (ii)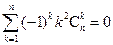 ; (iii)
; (iii)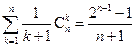 。
。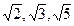 不能为同一等差数列的三项.
不能为同一等差数列的三项. 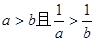 ,则
,则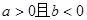 .
.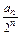 (n=1,2,…),求证:数列{cn}是等差数列;
(n=1,2,…),求证:数列{cn}是等差数列;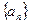 中,
中,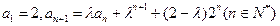 ,其中
,其中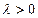 ,求数列
,求数列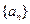 的通项公式
的通项公式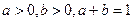 求证:
求证: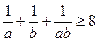 (用两种方法证明).
(用两种方法证明).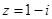 (
(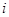 为虚数单位),则复数
为虚数单位),则复数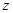 的模
的模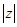 = .
= . ,则
,则

 则正确的结论是( )
则正确的结论是( )


 大小不定
大小不定