题目内容
设f(n)=1+
+
+…+
，是否存在g（n），使等式f（1）+f（2）+…+f（n-1）=g（n）[f（n）-1]对n≥2的一切自然数都成立，并证明你的结论．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
由于f（1）=1，f（2）=1+
，f（3）=1+
+
，…，f（n）=1+
+
+…+
，
所以f（1）+f（2）+f（3）+…+f（n-1）
=（n-1）×1+（n-2）×
+（n-3）×
+…+[n-（n-2）]×
+[n-（n-1）]×
=n[1+
+
+…+
]-（n-1）×1=n（
+
+
+…+
），
而g（n）[f（n）-1]=g（n）[（1+
+
+…+
）-1]=g（n）（
+
+
+…+
），
故由等式f（1）+f（2）+…+f（n-1）=g（n）[f（n）-1]，
可得n（
+
+
+…+
）=g（n）（
+
+
+…+
），
解得g（n）=n，
故存在g（n）满足条件，且通项公式为 g（n）=n．
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
所以f（1）+f（2）+f（3）+…+f（n-1）
=（n-1）×1+（n-2）×
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-2 |
| 1 |
| n-1 |
=n[1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
而g（n）[f（n）-1]=g（n）[（1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
故由等式f（1）+f（2）+…+f（n-1）=g（n）[f（n）-1]，
可得n（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
解得g（n）=n，
故存在g（n）满足条件，且通项公式为 g（n）=n．
练习册系列答案
相关题目
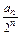(n=1,2,…),求证：数列{cn}是等差数列；
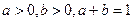求证：
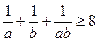（用两种方法证明）.
、
，定义
，其中
是
、
、
，有如下四个命题：
；
；
；
.
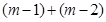i（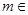
R）是纯虚数，则实数
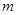等于（ ）
，求证：
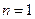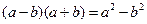
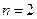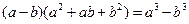
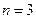时，有
时，有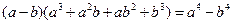
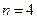时，有
时，有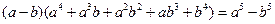
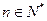时，你能得到的结论是： ．