题目内容
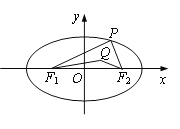
【题目】在平面直角坐标系xOy中,已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() .点
.点![]() 是椭圆
是椭圆![]() 在
在![]() 轴上方的动点,且△
轴上方的动点,且△![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 到△
到△![]() 三边的距离均相等.
三边的距离均相等.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②求证:点![]() 在定椭圆上.
在定椭圆上.
【答案】(1) ![]() ;(2)①
;(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】试题分析:(1)由题意可得![]() 的值,再由隐含条件求得
的值,再由隐含条件求得![]() ,则椭圆方程可求;(2)①求出
,则椭圆方程可求;(2)①求出![]() 点坐标,设出
点坐标,设出![]() 的坐标,结合点
的坐标,结合点![]() 到
到![]() 三边的距离均相等列方程组求得点
三边的距离均相等列方程组求得点![]() 的坐标;②根据三角形面积以及椭圆的定义列方程组,可得
的坐标;②根据三角形面积以及椭圆的定义列方程组,可得![]() ,
, ![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() , 所以点
, 所以点![]() 在定椭圆上.
在定椭圆上.
试题解析:(1)依题意, ![]() ,
, ![]() ,所以
,所以![]() ,从而
,从而![]() , 故椭圆方程为
, 故椭圆方程为![]() ,(2)①当
,(2)①当![]() 时,
时, ![]() , 则直线
, 则直线![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为:
的方程为: ![]() ,
,
所以![]() ,且
,且![]() ,其中
,其中![]() ,解得
,解得![]() ,
, ![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() ;
;
②设![]() ,则点
,则点![]() 到△
到△![]() 三边的距离均为
三边的距离均为![]() ,由
,由![]() ,
,
得![]() ,其中
,其中![]() ,所以
,所以![]() ,则直线
,则直线![]() 的方程为:
的方程为: ![]() ,即
,即![]() , 所以
, 所以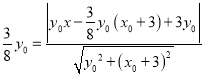 ,且
,且![]() , 且
, 且![]() , 化简得,
, 化简得, 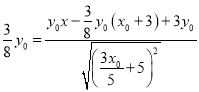 ,解得
,解得![]() ,
,
将![]() ,
, ![]() 代入
代入![]() ,得
,得![]() , 所以点
, 所以点![]() 在定椭圆上.
在定椭圆上.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目