Question

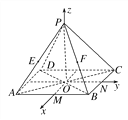
【题目】如图，正四棱锥P－ABCD中，底面边长为2，侧棱长为，M，N分别为AB，BC的中点，以O为原点，射线OM，ON，OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系．若E，F分别为PA，PB的中点，求A，B，C，D，E，F的坐标．

Answer 1

【答案】A(1，－1,0)，B(1,1,0)，C(－1,1,0)，D(－1，－1,0)， E，F.

【解析】试题分析:先确定各点坐标,再根据中点坐标公式求解

试题解析:

∵正四棱锥P－ABCD中，底面边长为2，侧棱长为，

∴OB＝，OP＝＝＝2，

∴由上可得A(1，－1,0)，B(1,1,0)，C(－1,1,0)，D(－1，－1,0)，P(0,0,2)．

又∵E，F分别为PA，PB的中点，

∴由中点坐标公式可得E，F.