Question

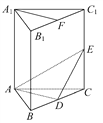
【题目】如图，已知四棱锥的底面为矩形，D为

的中点，AC⊥平面BCC1B1．

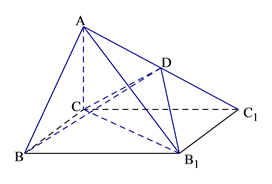
（Ⅰ）证明：AB//平面CDB1;

（Ⅱ）若AC=BC=1，BB1=,

（1）求BD的长；

（2）求三棱锥C-DB1C1的体积.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）（1）; （2）.

【解析】试题分析：（Ⅰ）利用中位线定理得出DE//AB，即可证得；

（Ⅱ）（1）在中，利用勾股定理运算即可；

（2）由平面.利用求解即可.

试题解析：

（Ⅰ）证明：连结交于E，连结DE，

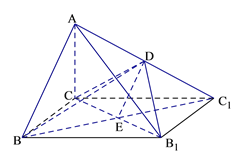
∵D、E分别为和的中点，

∴DE//AB,

又∵平面, 平面,

∴AB//平面CDB1;

（Ⅱ）（1）∵AC⊥平面BCC1B1， 平面，

∴,

又∵, ，

∴平面，

∵平面,

∴,

在,∵BC=1， ,

∴;

（2）解法1：∵平面，BC//B1C1

∴平面,

∴ .

【解法2：取中点F,连结DF，

∵DF为△的中位线，∴DF//AC,

∵平面，从而可得平面,

∴ .