题目内容
【题目】【2016高考江苏卷】已知函数![]() .设
.设![]() .
.
(1)求方程![]() 的根;
的根;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若![]() ,函数
,函数![]() 有且只有1个零点,求
有且只有1个零点,求![]() 的值。
的值。
【答案】(1)①0 ②4(2)1
【解析】
试题分析:(1)①根据指数间倒数关系![]() 转化为一元二次方程
转化为一元二次方程![]() ,求方程根②根据指数间平方关系
,求方程根②根据指数间平方关系![]() ,将不等式转化为一元不等式,再利用变量分离转化为对应函数最值,即
,将不等式转化为一元不等式,再利用变量分离转化为对应函数最值,即![]() 的最小值,最后根据基本不等式求最值(2)先分析导函数零点情况:唯一零点
的最小值,最后根据基本不等式求最值(2)先分析导函数零点情况:唯一零点![]() ,再确定原函数单调变化趋势:先减后增,从而结合图像确定唯一零点必在极值点
,再确定原函数单调变化趋势:先减后增,从而结合图像确定唯一零点必在极值点![]() 取得,而
取得,而![]() ,因此极值点
,因此极值点![]() 必等于零,进而求出
必等于零,进而求出![]() 的值.本题难点在证明
的值.本题难点在证明![]() ,这可利用反证法:若
,这可利用反证法:若![]() ,则可寻找出一个区间
,则可寻找出一个区间![]() ,由
,由![]() 结合零点存在定理可得函数存在另一零点,与题意矛盾,其中可取
结合零点存在定理可得函数存在另一零点,与题意矛盾,其中可取![]() ;若
;若![]() ,同理可得.
,同理可得.
试题解析:(1)因为![]() ,所以
,所以![]() .
.
①方程![]() ,即
,即![]() ,亦即
,亦即![]() ,
,
所以![]() ,于是
,于是![]() ,解得
,解得![]() .
.
②由条件知![]() .
.
因为![]() 对于
对于![]() 恒成立,且
恒成立,且![]() ,
,
所以![]() 对于
对于![]() 恒成立.
恒成立.
而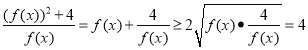 ,且
,且![]() ,
,
所以![]() ,故实数
,故实数![]() 的最大值为4.
的最大值为4.
(2)因为函数![]() 只有1个零点,而
只有1个零点,而![]() ,
,
所以0是函数![]() 的唯一零点.
的唯一零点.
因为![]() ,又由
,又由![]() 知
知![]() ,
,
所以![]() 有唯一解
有唯一解![]() .
.
令![]() ,则
,则![]() ,
,
从而对任意![]() ,
,![]() ,所以
,所以![]() 是
是![]() 上的单调增函数,
上的单调增函数,
于是当![]() ,
,![]() ;当
;当![]() 时,
时,![]() .
.
因而函数![]() 在
在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数.
上是单调增函数.
下证![]() .
.
若![]() ,则
,则![]() ,于是
,于是![]() ,
,
又![]() ,且函数
,且函数![]() 在以
在以![]() 和
和![]() 为端点的闭区间上的图象不间断,所以在
为端点的闭区间上的图象不间断,所以在![]() 和
和![]() 之间存在
之间存在![]() 的零点,记为
的零点,记为![]() . 因为
. 因为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 与“0是函数
与“0是函数![]() 的唯一零点”矛盾.
的唯一零点”矛盾.
若![]() ,同理可得,在
,同理可得,在![]() 和
和![]() 之间存在
之间存在![]() 的非0的零点,矛盾.
的非0的零点,矛盾.
因此,![]() .
.
于是![]() ,故
,故![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目