题目内容
19.在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(2,1)=60.分析 利用二项式定理列出xmyn项的系数为f(m,n).然后求解即可.
解答 解:(1+x)6(1+y)4的展开式中,通项公式${C}_{6}^{m}{C}_{4}^{n}{x}^{m}{y}^{n}$.
则x2y项的系数:f(2,1)=${C}_{6}^{2}{C}_{4}^{1}$=60.
故答案为:60.
点评 本题考查二项式定理的应用,通项公式的灵活运用,考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
14.已知函数f(x)=x2•sinx,各项均不相等的数列{xn}满足|xi|≤$\frac{π}{2}$(i=1,2,3,…,n).令F(n)=(x1+x2+…+xn)•[f(x1)+f(x2)+…f(xn)](n∈N*).给出下列三个命题:
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
4.从1,2,2,3,3,3这六个数字中任取5个,组成五位数,则不同的五位数共有( )
| A. | 50个 | B. | 60个 | C. | 100个 | D. | 120个 |
11.函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴为( )
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
8.等差数列{an}的前n项和为Sn,且a1+a2=10,S4=36,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量是( )
| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
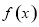 在
在 上是增函数,则满足
上是增函数,则满足 的实数
的实数 的取值范围是______________.
的取值范围是______________.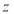 满足
满足 ,则
,则 ( )
( )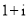 B.
B.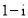
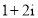 D.
D.