题目内容
6.已知直线l:x+y+m=0(m∈R)与圆C:(x+2)2+(y-1)2=4相交于A、B两点,则$\overrightarrow{AC}$•$\overrightarrow{AB}$的最大值为8.分析 取线段AB的中点为D,则由题意可得CD⊥AB,则$\overrightarrow{AC}$•$\overrightarrow{AB}$=$\frac{1}{2}$AB2.故当弦长AB最大(为圆的直径)时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大,由此求得$\overrightarrow{AC}$•$\overrightarrow{AB}$的最大值.
解答 解:取线段AB的中点为D,则由题意可得CD⊥AB,则$\overrightarrow{AC}$•$\overrightarrow{AB}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|=$\frac{1}{2}$•${\overrightarrow{AB}}^{2}$=$\frac{1}{2}$AB2.
故当弦长AB最大时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大,即当圆心C(-2,1)在直线l:x+y+m=0上时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大.
把圆心C(-2,1)代入直线l:x+y+m=0,求得m=1,
故$\overrightarrow{AC}$•$\overrightarrow{AB}$的最大值为 $\frac{1}{2}$AB2=$\frac{1}{2}$(2r)2=2r2=2×4=8,
故答案为:8.
点评 本题主要考查直线和圆相交的性质,两个向量的数量积的定义,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
14.已知函数f(x)=x2•sinx,各项均不相等的数列{xn}满足|xi|≤$\frac{π}{2}$(i=1,2,3,…,n).令F(n)=(x1+x2+…+xn)•[f(x1)+f(x2)+…f(xn)](n∈N*).给出下列三个命题:
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
1.2014巴西世界杯结束后,某网站针对世界杯情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定;观看世界杯直播32场(含)以下者,称为“非球迷”,观看比赛直播超过32场这成为“球迷”,得到如下统计表:
若参与调查的“非球迷”总人数为7600人.
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
11.函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴为( )
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
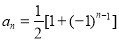

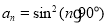
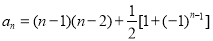
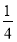 圆弧)( )
圆弧)( )
 B.
B.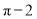
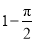 D.
D.