题目内容
2.某几何体的三视图如图所示,则此几何体的对应直观图中△PAB的面积为$\sqrt{7}$.
分析 画出几何体的直观图,然后利用三视图的数据求解即可.
解答  解:几何体的直观图如图:底面是边长为2的正三角形,高为2,顶点P在底面的射影是正三角形的已改顶点,直观图中△PAB是等腰三角形,斜高为:$\sqrt{{2}^{2}+{(\sqrt{3})}^{2}}$=$\sqrt{7}$,△PAB的面积为:$\frac{1}{2}×2×\sqrt{7}=\sqrt{7}$.
解:几何体的直观图如图:底面是边长为2的正三角形,高为2,顶点P在底面的射影是正三角形的已改顶点,直观图中△PAB是等腰三角形,斜高为:$\sqrt{{2}^{2}+{(\sqrt{3})}^{2}}$=$\sqrt{7}$,△PAB的面积为:$\frac{1}{2}×2×\sqrt{7}=\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查三视图与直观图的关系,直观图的侧面面积的求法,考查计算能力.

练习册系列答案
相关题目
14.已知函数f(x)=x2•sinx,各项均不相等的数列{xn}满足|xi|≤$\frac{π}{2}$(i=1,2,3,…,n).令F(n)=(x1+x2+…+xn)•[f(x1)+f(x2)+…f(xn)](n∈N*).给出下列三个命题:
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
10. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
17.已知函数f(x)=sinπx和函数g(x)=cosπx在区间[0,2]上的图象交于A,B两点,则△OAB面积是( )
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
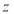 满足
满足 ,则
,则 ( )
( )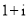 B.
B.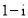
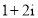 D.
D.

 ,且
,且 .
. 在区间
在区间 上单调递增;
上单调递增; ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.