Question

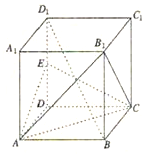
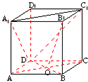
如图，在边长为a的正方体ABCD-A₁B₁C₁D₁中，E，F，G，H分别是CC₁，C₁D₁，D₁D，CD的中点，N是BC的中点，M在四边形EFGH上及其内部运动，若MN∥平面A₁BD，则点M轨迹的长度是______．

Answer 1

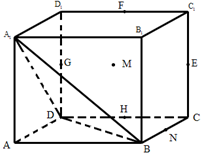
连接GH、HN，则GH∥BA₁，HN∥BD，
∵在边长为a的正方体ABCD-A₁B₁C₁D₁中，E，F，G，H分别是CC₁，C₁D₁，D₁D，CD的中点，
N是BC的中点，M在四边形EFGH上及其内部运动，MN∥平面A₁BD，
∴平面A₁BD∥平面GHN，
又点M在四边形上及其内部运动，
则点M须在线段GH上运动，即满足条件，GH=

2

2

a，
则点M轨迹的长度是

2

2

a．
故答案为：

2

2

a．