题目内容
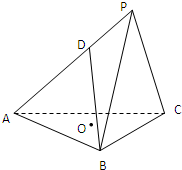
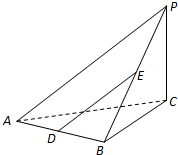
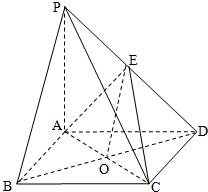
设四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥面ABCD,PA=AB,E为PD的中点.
(1)求证:直线PB∥面ACE
(2)求证:直线AE⊥面PCD
(3)求直线AC与平面PCD所成角的大小.
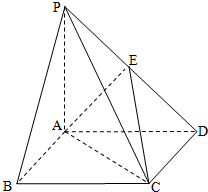
(1)求证:直线PB∥面ACE
(2)求证:直线AE⊥面PCD
(3)求直线AC与平面PCD所成角的大小.

(1)连接BD交AC于点O,连接OE
易知:O为BD的中点
而E为PD的中点
∴OE∥PB
又PB不在平面ACE内,OE在平面ACE内
∴PB∥平面ACE…(4分)
(2)证明:∵PA⊥面ABCD
∴PA⊥CD
又正方形ABCD
∴CD⊥AD
∴CD⊥面PAD故:CD⊥AE
∵在直角三角形PAD中,PA=AB=AD,E为PD的中点∴AE⊥PD
∴AE⊥面PCD…(8分)
(3)由(2)知:AC在面PCD内的射影为CE
故直线AC与平面PCD所成角为∠ACE…(10分)
由于PA=AB=AD=2,在直角三角形ACF中,易知:AE=
,AC=2
∴sin∠ACE=
=
∴∠ACE=30°
即:直线AC与平面PCD所成角的大小为30°…(12分)
易知:O为BD的中点
而E为PD的中点
∴OE∥PB
又PB不在平面ACE内,OE在平面ACE内
∴PB∥平面ACE…(4分)
(2)证明:∵PA⊥面ABCD
∴PA⊥CD
又正方形ABCD
∴CD⊥AD
∴CD⊥面PAD故:CD⊥AE
∵在直角三角形PAD中,PA=AB=AD,E为PD的中点∴AE⊥PD
∴AE⊥面PCD…(8分)
(3)由(2)知:AC在面PCD内的射影为CE
故直线AC与平面PCD所成角为∠ACE…(10分)
由于PA=AB=AD=2,在直角三角形ACF中,易知:AE=
| 2 |
| 2 |
∴sin∠ACE=
| AE |
| AC |
| 1 |
| 2 |
即:直线AC与平面PCD所成角的大小为30°…(12分)


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目