题目内容
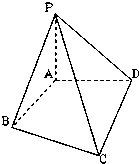
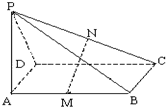
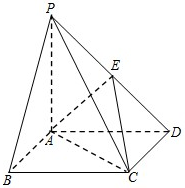
如图,在四棱锥P-ABCD中,PD垂直于底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=90°,且AB=2AD=2DC=2PD=4,E为PA的中点.
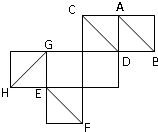
(1)如图,若正视方向与AD平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
(2)证明:DE∥平面PBC;
(3)求四棱锥P-ABCD的体积.
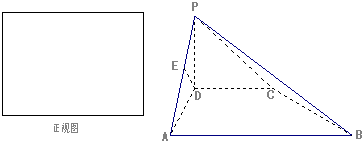
(1)如图,若正视方向与AD平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
(2)证明:DE∥平面PBC;
(3)求四棱锥P-ABCD的体积.

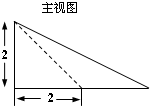
解(1)正视图如下:(没标数据扣1分)…(3分)
主视图面积S=
×4×2=4cm2…(5分)
(2)设PB的中点为F,连接EF,CF…(6分)
∵E,F分别是PA,PB的中点
∴EF∥AB
又DC∥AB∴EF∥DC
且EF=DC=
AB…(8分)
故四边形CDEF是平行四边形,
即可得ED∥CF,(9分)
又ED?平面PBC,CF?平面,
∴ED∥平面PBC(10分)
(3)∵PD⊥底面ABCD,∴PD=2是四棱锥P-ABCD的高(11分)
∵AB=4,DC=2,AD=2
∴直角梯形ABCD的面积是S底=
AD•(AB+DC)=
×2×(2+4)=6(cm2)(13分)
∴四棱锥P-ABCD的体积是V=
S底•PD=
×6×2=4
(14分)
主视图面积S=
| 1 |
| 2 |
(2)设PB的中点为F,连接EF,CF…(6分)
∵E,F分别是PA,PB的中点
∴EF∥AB
又DC∥AB∴EF∥DC
且EF=DC=
| 1 |
| 2 |
故四边形CDEF是平行四边形,
即可得ED∥CF,(9分)
又ED?平面PBC,CF?平面,
∴ED∥平面PBC(10分)
(3)∵PD⊥底面ABCD,∴PD=2是四棱锥P-ABCD的高(11分)
∵AB=4,DC=2,AD=2
∴直角梯形ABCD的面积是S底=
| 1 |
| 2 |
| 1 |
| 2 |
∴四棱锥P-ABCD的体积是V=
| 1 |
| 3 |
| 1 |
| 3 |
|


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目