题目内容
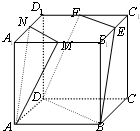
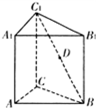
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
(Ⅰ)当点P为AB的中点时,证明DP∥平面ACC1A1;
(Ⅱ)若AP=3PB,求三棱锥B-CDP的体积.
(Ⅰ)当点P为AB的中点时,证明DP∥平面ACC1A1;
(Ⅱ)若AP=3PB,求三棱锥B-CDP的体积.

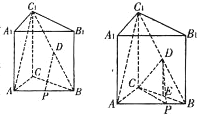
(I)连接DP、AC1,
∵△ABC1中,P、D分别为AB、BC1中点
∴DP∥AC1,
∵AC1⊆平面ACC1A1,DP?平面ACC1A1,
∴DP∥平面ACC1A1
(II)由AP=3PB,得PB=
AB=
过点D作DE⊥BC于E,则DE∥CC1且DE=
CC1
又∵CC1⊥平面ABC,∴DE⊥平面BCP
∵CC1=3,∴DE=
∵S△BCP=
×2×
×sin60°=
∴三棱锥B-CDP的体积v=
×
×
=
∵△ABC1中,P、D分别为AB、BC1中点
∴DP∥AC1,
∵AC1⊆平面ACC1A1,DP?平面ACC1A1,
∴DP∥平面ACC1A1
(II)由AP=3PB,得PB=
| 1 |
| 4 |
| 1 |
| 2 |
过点D作DE⊥BC于E,则DE∥CC1且DE=
| 1 |
| 2 |
又∵CC1⊥平面ABC,∴DE⊥平面BCP
∵CC1=3,∴DE=
| 3 |
| 2 |
∵S△BCP=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴三棱锥B-CDP的体积v=
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 2 |
| ||
| 8 |


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目