Question

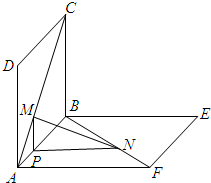
如图，已知边长都为1正方形ABCD与正方形ABEF，∠DAF=90°，M，N分别是对角线AC和BF上的点，且AM=FN=a(0＜a＜

2

)．
（1）求证：MN∥平面BCE；
（2）求MN的最小值．

Answer 1

（1）证明：过M作MP⊥AB，垂足为P，连接PN．
∵

AM

MC

=

AP

PB

，又

AM

MC

=

FN

NB

∴

AP

PB

=

FN

NB

[（2分）]
∴PN∥AF
∴平面MPN∥平面CBE[（4分）]
从而MN∥平面BCE[（6分）]
（2）∠MPN=90°MP=

2

2

a，PN=1-

2

2

a[（8分）]
由勾股定理知：MN2=MP2+PN2=a2-

2

a+1=(a-

2

2

)2+

1

2

[（10分）]
当a=

2

2

a时，MN的最小值为

2

2

．[（12分）]