题目内容
已知f(x),g(x)都是定义在R上的函数,g(x)≠0,若f'(x)g(x)<f(x)g'(x),且f(x)=ax•g(x)(a>0且a≠1)及
+
=
,则a的值为______.
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 10 |
| 3 |
∵f(x)=ax•g(x)
∴
=ax,得
=a,
=a-1=
因此
+
=
即a+
=
解之得a=3或
设F(x)=
,则F'(x)=
∵f'(x)g(x)<f(x)g'(x),
∴F'(x)=
<0在R上成立,故F(x)是R上的减函数
即y=ax是R上的减函数,故a∈(0,1)
所以实数a的值为
故答案为:
∴
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 1 |
| a |
因此
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 10 |
| 3 |
| 1 |
| a |
| 10 |
| 3 |
解之得a=3或
| 1 |
| 3 |
设F(x)=
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g′(x) |
∵f'(x)g(x)<f(x)g'(x),
∴F'(x)=
| f′(x)g(x)-f(x)g′(x) |
| g′(x) |
即y=ax是R上的减函数,故a∈(0,1)
所以实数a的值为
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |

练习册系列答案
相关题目
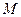 是由满足下列两个条件的函数
是由满足下列两个条件的函数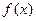 构成的集合:①方程
构成的集合:①方程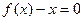 有实根; ②函数
有实根; ②函数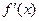 满足
满足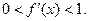 (1)判断函数
(1)判断函数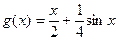 是不是集合
是不是集合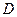 ,对于任意
,对于任意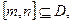 都存在
都存在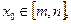 使得等式
使得等式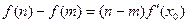 成立.”试用这一性质证明:方程
成立.”试用这一性质证明:方程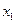 是方程
是方程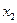 ,
,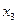 ,当
,当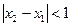 ,且
,且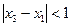 时,
时, 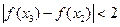 .
.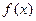 的图象与函数
的图象与函数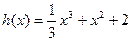 的图象关于点A(0,1对称.(Ⅰ)求
的图象关于点A(0,1对称.(Ⅰ)求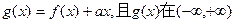 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.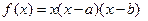 ,
,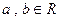 。
。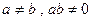 ,过两点
,过两点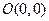 和
和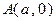 的中点作
的中点作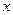 轴的垂线交曲线
轴的垂线交曲线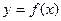 于点
于点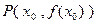 ,求证:曲线
,求证:曲线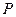 处的切线
处的切线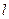 过点
过点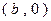 ;
;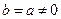 ,当
,当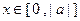 时
时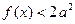 恒成立,求实数
恒成立,求实数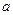 的取值范围。
的取值范围。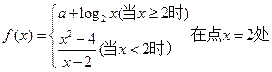 连续,则常数
连续,则常数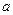 的值是( )
的值是( )