题目内容
已知函数f(x)的导函数为f′(x),且f(x)=2xf′(1)+lnx,则f′(1)=______.
求导得:f′(x)=2f′(1)+
,
令x=1,得到f′(1)=2f′(1)+1,
解得:f′(1)=-1,
∴f(x)=-2x+lnx,
则f(1)=-2+ln1=-2.
故答案为-2.
| 1 |
| x |
令x=1,得到f′(1)=2f′(1)+1,
解得:f′(1)=-1,
∴f(x)=-2x+lnx,
则f(1)=-2+ln1=-2.
故答案为-2.

练习册系列答案
相关题目
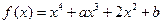 (
(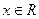 ),其中
),其中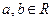 .(Ⅰ)当
.(Ⅰ)当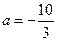 时,讨论函数
时,讨论函数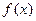 的单调性;(Ⅱ)若函数
的单调性;(Ⅱ)若函数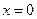 处有极值,求
处有极值,求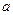 的取值范围;(Ⅲ)若对于任意的
的取值范围;(Ⅲ)若对于任意的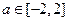 ,不等式
,不等式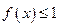 在
在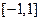 上恒成立,求
上恒成立,求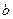 的取值范围.
的取值范围. ,若
,若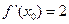 ,则
,则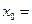 ( )
( )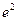


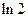
 ,若,
,若,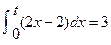 ,则
,则 。
。