题目内容
设函数f（x）的导数为f′（x），且f（x）=2x-f′（1）lnx+f′（2），则f′（2）的值是______．
由f（x）=2x-f′（1）lnx+f′（2），得
f′(x)=2xln2-
，取x=1得：f′（1）=2ln2-f′（1）．
∴f′（1）=ln2．
则f′(x)=2xln2-
，
∴f′(2)=4ln2-
=
ln2．
故答案为：
ln2．
f′(x)=2xln2-
| f′(1) |
| x |
∴f′（1）=ln2．
则f′(x)=2xln2-
| ln2 |
| x |
∴f′(2)=4ln2-
| ln2 |
| 2 |
| 7 |
| 2 |
故答案为：
| 7 |
| 2 |
练习册系列答案
相关题目
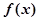满足：①在
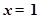时有极值；②图像过点
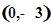，且在该点处的切线与直线
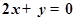平行．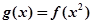
的单调递增区间．
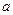为实数，函数
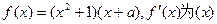的导函数。(1)若
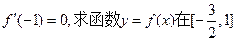上的最大值和最小值；(2)若函数
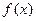有两个不同的极值点，求