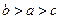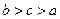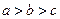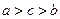题目内容
(本小题满分14分)
已知定义域为[0, 1]的函数f(x)同时满足:
①对于任意的x [0, 1],总有f(x)≥0;
[0, 1],总有f(x)≥0;
②f(1)=1;
③若0≤x1≤1, 0≤x2≤1, x1+x2≤1, 则有f(x1+x2) ≥ f(x1)+f(x2).
(1)试求f(0)的值;
(2)试求函数f(x)的最大值;
(3)试证明:当x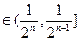 , n
, n N+时,f(x)<2x.
N+时,f(x)<2x.
已知定义域为[0, 1]的函数f(x)同时满足:
①对于任意的x
 [0, 1],总有f(x)≥0;
[0, 1],总有f(x)≥0; ②f(1)=1;
③若0≤x1≤1, 0≤x2≤1, x1+x2≤1, 则有f(x1+x2) ≥ f(x1)+f(x2).
(1)试求f(0)的值;
(2)试求函数f(x)的最大值;
(3)试证明:当x
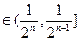 , n
, n N+时,f(x)<2x.
N+时,f(x)<2x.(1)f(0)=0
(2)f(x)取最大值1.
(3)略
(2)f(x)取最大值1.
(3)略
(1)令x1=x2=0,依条件(3)可得f(0+0)≥2f(0),即f(0)≤0
又由条件(1)得f(0)≥0 故f(0)=0 …………3分
(2)任取0≤x1<x2≤1可知x2-x1 (0,1],则
(0,1],则
f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)≥f(x1)
于是当0≤x≤1时,有f(x)≤f(1)=1因此当x=1时,f(x)取最大值1.…………8分
(3)证明:先用数学归纳法证明:当x
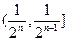 (n
(n N+)时,f(x)≤
N+)时,f(x)≤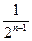
10当n=1时,x
 ,f(x)≤f(1)=1=
,f(x)≤f(1)=1=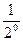 ,不等式成立.
,不等式成立.
当n=2时,x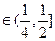 ,
,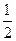 <2x≤1,f(2x)≤1,f(2x)≥f(x)+f(x)=2f(x)
<2x≤1,f(2x)≤1,f(2x)≥f(x)+f(x)=2f(x)
∴f(x)≤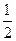 f(2x)≤
f(2x)≤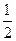 不等式成立.
不等式成立.
20假设当n=k(k N+,k≥2)时,不等式成立,即x
N+,k≥2)时,不等式成立,即x
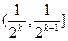 时,f(x)≤
时,f(x)≤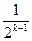
则当n=k+1时,x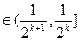 ,记t=2x,则t=2x
,记t=2x,则t=2x
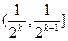 , ∴f(t)≤
, ∴f(t)≤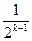
而f(t)=f(2x)≥2f(x),∴f(x)≤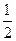 f(2x)=
f(2x)=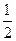 f(t)≤
f(t)≤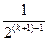
因此当n=k+1时不等式也成立.
由10,20知,当x
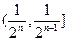 (n
(n N+)时,f(x)≤
N+)时,f(x)≤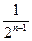
又当x
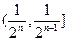 (n
(n N+)时,2x>
N+)时,2x>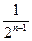 , 此时f(x)<2x.
, 此时f(x)<2x.
综上所述:当x
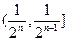 (n
(n N+)时,有f(x)<2x. ………… 14分
N+)时,有f(x)<2x. ………… 14分
又由条件(1)得f(0)≥0 故f(0)=0 …………3分
(2)任取0≤x1<x2≤1可知x2-x1
 (0,1],则
(0,1],则 f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)≥f(x1)
于是当0≤x≤1时,有f(x)≤f(1)=1因此当x=1时,f(x)取最大值1.…………8分
(3)证明:先用数学归纳法证明:当x

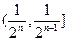 (n
(n N+)时,f(x)≤
N+)时,f(x)≤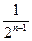
10当n=1时,x

 ,f(x)≤f(1)=1=
,f(x)≤f(1)=1=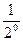 ,不等式成立.
,不等式成立.当n=2时,x
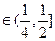 ,
,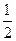 <2x≤1,f(2x)≤1,f(2x)≥f(x)+f(x)=2f(x)
<2x≤1,f(2x)≤1,f(2x)≥f(x)+f(x)=2f(x)∴f(x)≤
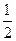 f(2x)≤
f(2x)≤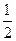 不等式成立.
不等式成立.20假设当n=k(k
 N+,k≥2)时,不等式成立,即x
N+,k≥2)时,不等式成立,即x
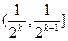 时,f(x)≤
时,f(x)≤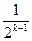
则当n=k+1时,x
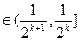 ,记t=2x,则t=2x
,记t=2x,则t=2x
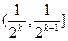 , ∴f(t)≤
, ∴f(t)≤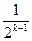
而f(t)=f(2x)≥2f(x),∴f(x)≤
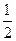 f(2x)=
f(2x)=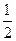 f(t)≤
f(t)≤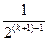
因此当n=k+1时不等式也成立.
由10,20知,当x

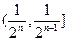 (n
(n N+)时,f(x)≤
N+)时,f(x)≤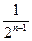
又当x

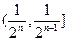 (n
(n N+)时,2x>
N+)时,2x>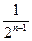 , 此时f(x)<2x.
, 此时f(x)<2x.综上所述:当x

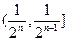 (n
(n N+)时,有f(x)<2x. ………… 14分
N+)时,有f(x)<2x. ………… 14分
练习册系列答案
相关题目
 是定义在(1,4)上单调递减函数,且
是定义在(1,4)上单调递减函数,且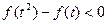 ,求
,求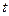 的取值范围。
的取值范围。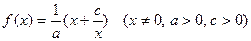 ,当
,当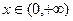 时,函数
时,函数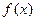 在x=2处取得最小值1。
在x=2处取得最小值1。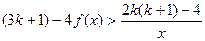 。
。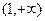 上不是增函数的是 ( )
上不是增函数的是 ( )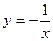 ;
;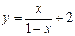 ;
;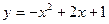 ;
;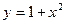 .
.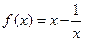 ,对任意的
,对任意的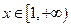 ,
,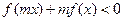 恒成立,则实数
恒成立,则实数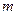 的取值范围是____________.
的取值范围是____________.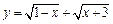 的最大值为M,最小值为m,则
的最大值为M,最小值为m,则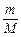 的值为( )
的值为( )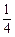
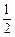
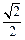
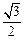
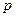 :关于
:关于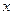 的函数
的函数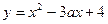 在[1,+∞)上是增函数,命题
在[1,+∞)上是增函数,命题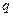 :关于
:关于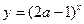 在R上为减函数,若
在R上为减函数,若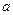 的取值范围是 ( )
的取值范围是 ( )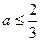
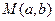 在函数
在函数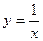 的图象上,点
的图象上,点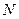 与点
与点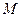 关于
关于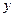 轴对称且在直线
轴对称且在直线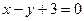
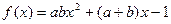 在区间
在区间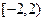 上 ( )
上 ( )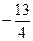 ,无最大值
,无最大值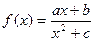 的图象如图所示,则
的图象如图所示,则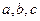 的大
的大 小关系是
小关系是