题目内容

4．设a=${log}_{2}{\frac{1}{3}}$，b=${e}^{-\frac{1}{3}}$，c=lnπ，则（　　）
A．c＜a＜bB．a＜c＜bC．a＜b＜cD．b＜a＜c

分析 利用指数函数与对数函数的单调性即可得出．

解答 解：∵a=${log}_{2}{\frac{1}{3}}$＜0，0＜b=${e}^{-\frac{1}{3}}$＜1，c=lnπ＞1，
∴a＜b＜c．
故选：C．

点评 本题考查了指数函数与对数函数的单调性，属于基础题．

练习册系列答案
相关题目
14．已知甲、乙、丙、丁、戊、己等6人，分别求解下列问题（用数字作答）：
（1）若他们排成一排，则甲、乙、丙三人中任两人都不相邻的不同排法有多少种；
（2）若派遣这6人去参加一项会议，至少有一人去，去几人自行决定，但甲与乙两人要么同时去，要么同时不去，求共有多少种不同的派遣方法；
（3）若这6人中，有4名男生，2名女生，现从中选出4人去参加某项活动，要求男女生都有，求不同的选法种数．
15．$\frac{3+2i}{2-3i}$（　　）
A．-iB．iC．1+iD．1-i
12．某个海边旅游景点，有小型游艇出租供游客出海游玩，收费标准如下：租用时间不超过2小时收费100，超过2小时的部分按每小时100收取（不足一小时按一小时计算）．现甲、乙两人独立来该景点租用小型游艇，各租一次．设甲、乙租用不超过两小时的概率分别为$\frac{1}{3}$，$\frac{1}{2}$；租用2小时以上且不超过3小时的概率分别为$\frac{1}{2}$，$\frac{1}{3}$，且两人租用的时间都不超过4小时．
（Ⅰ）求甲、乙两人所付费用相同的概率；
（Ⅱ）设甲、乙两人所付的费用之和为随机变量ξ，求ξ的分布列与数学期望．
19．已知点A（sinθ，1），B（cosθ，0），C（-sinθ，2），且$\overrightarrow{AB}=\overrightarrow{BP}$．
（Ⅰ）记函数$f（θ）=\overrightarrow{BP}•\overrightarrow{CA}$，$θ∈（-\frac{π}{8}，\frac{π}{2}）$，讨论函数的单调性，并求其值域；
（Ⅱ）若O，P，C三点共线，求$|\overrightarrow{OA}+\overrightarrow{OB}|$的值．
9．设函数f（x）=sin（ωx+φ）（ω，φ是常数，ω＞0）．若f（x）在区间[$\frac{1}{3}$，1]上具有单调性，且f（0）=f（$\frac{2}{3}$）=-f（1），则下列有关f（x）的每题正确的有
①②④
（请填上所有正确命题的序号）．
①f（x）的最小周期为2；    
②x=$\frac{1}{3}$是 f（x）的对称轴；
③f（x）在[1，$\frac{5}{3}$]上具有单调性；  
④y=f（x+$\frac{5}{6}$）为奇函数．
16．已知命题p：sinα-cosα=$\sqrt{2}$，命题q：双曲线$\frac{{x}^{2}}{co{s}^{2}α}$-$\frac{{y}^{2}}{si{n}^{2}α}$=1的渐近线与圆x2+（y-1）2=$\frac{1}{2}$相切，则命题p为命题q为（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．已知函数f（x）=|2x+1|+|2x-3|，若关于x的不等式f（x）＜|a-1|的解集非空，则实数a的取值范围是（　　）
A．[-3，5]B．（-3，5）C．（-∞，-3]∪[5，+∞）D．（-∞，-3）∪（5，+∞）
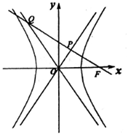14．如图，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的右焦点，过F作渐近线的垂线，垂足为P，与另一条渐近线相交于Q，若|PF|=|PQ|，则C的离心率为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网