题目内容
9.设函数f(x)=sin(ωx+φ)(ω,φ是常数,ω>0).若f(x)在区间[$\frac{1}{3}$,1]上具有单调性,且f(0)=f($\frac{2}{3}$)=-f(1),则下列有关f(x)的每题正确的有①②④
(请填上所有正确命题的序号).
①f(x)的最小周期为2;
②x=$\frac{1}{3}$是 f(x)的对称轴;
③f(x)在[1,$\frac{5}{3}$]上具有单调性;
④y=f(x+$\frac{5}{6}$)为奇函数.
分析 由题意可得可得函数f(x)的图象关于直线x=$\frac{1}{3}$对称,且一个相邻的对称中心为($\frac{5}{6}$,0),由此判断各个选项是否正确,从而得出结论.
解答 解:由f(0)=f($\frac{2}{3}$)=-f(1),可得函数f(x)的图象关于直线x=$\frac{0+\frac{2}{3}}{2}$=$\frac{1}{3}$对称,且一个对称中心为($\frac{5}{6}$,0).
故有$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{5}{6}$-$\frac{1}{3}$=$\frac{1}{2}$,故函数的周期为2,f(x+$\frac{5}{6}$)为奇函数,故①②④正确.
由以上可得ω=π,再结合 $\frac{5}{6}$•π+φ=kπ,k∈z,可取φ=$\frac{π}{6}$,f(x)=sin(πx+$\frac{π}{6}$).
在[1,$\frac{5}{3}$]上,πx+$\frac{π}{6}$∈[$\frac{7π}{6}$,$\frac{11π}{6}$],故f(x)在[1,$\frac{5}{3}$]上没有单调性,故③不对.
故答案为:①②④.
点评 本题主要考查正弦函数的图象特征,属于基础题.

练习册系列答案
相关题目
20.某三棱锥的三视图如图所示,图中网格小正方形的边长为1,则该三棱锥的体积为( )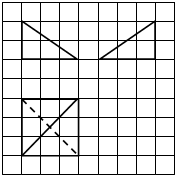

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
4.设a=${log}_{2}{\frac{1}{3}}$,b=${e}^{-\frac{1}{3}}$,c=lnπ,则( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<a<c |
14.在如图所示的茎叶图中,若甲组数据众数为14,则乙组数据的中位数为( )
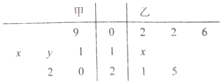

| A. | 6 | B. | 8 | C. | 10 | D. | 14 |
19.己知f(x)=x3-ax在[1,+∞)上是单调增函数,则a的取值范围是( )
| A. | (3,+∞) | B. | (1,3) | C. | (-∞,3) | D. | (-∞,3] |
 如图,矩形ABCD中,AB=2,BC=4,以矩形ABCD的中心为原点,过矩形ABCD的中心平行于BC的直线为x轴,建立直角坐标系,
如图,矩形ABCD中,AB=2,BC=4,以矩形ABCD的中心为原点,过矩形ABCD的中心平行于BC的直线为x轴,建立直角坐标系,