题目内容
数列{an}的前n项和Sn=2n-1,则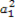 +
+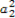 +
+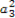 +…+
+…+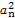 等于( )
等于( )
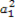 +
+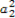 +
+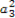 +…+
+…+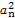 等于( )
等于( )| A.(2n-1)2 | B. (2n-1)2 (2n-1)2 |
| C.4n-1 | D. (4n-1) (4n-1) |
D
an=Sn-Sn-1=2n-1(n>1),又a1=S1=1=20,适合上式,∴an=2n-1(n∈N*),
∴{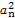 }是
}是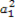 =1,q=22的等比数列,由求和公式得
=1,q=22的等比数列,由求和公式得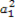 +
+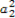 +
+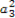 +…+
+…+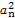 =
=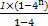 =
= (4n-1).
(4n-1).
∴{
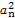 }是
}是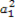 =1,q=22的等比数列,由求和公式得
=1,q=22的等比数列,由求和公式得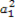 +
+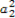 +
+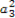 +…+
+…+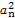 =
=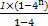 =
= (4n-1).
(4n-1).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )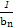 }的前n项和Tn.
}的前n项和Tn.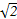

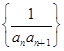 的前n项和为
的前n项和为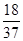 ,则n=________.
,则n=________. ,则S10等于( )
,则S10等于( )


