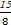题目内容
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an.若a1=1,a2=2,则数列{an}的通项公式是________.
an= (n∈N*)
(n∈N*)
 (n∈N*)
(n∈N*)设OAn=x(n≥3),OB1=y,∠O=θ,
记S△OA1B1= ×1×ysin θ=S,
×1×ysin θ=S,
那么S△OA2B2= ×2×2ysin θ=4S,
×2×2ysin θ=4S,
S△OA3B3=4S+(4S-S)=7S,
…,
S△OAnBn= x·xysin θ=(3n-2)S,
x·xysin θ=(3n-2)S,
∴ ,
,
∴ ,∴x=
,∴x= .即an=
.即an= (n≥3).
(n≥3).
经验证知an= (n∈N*).
(n∈N*).
记S△OA1B1=
 ×1×ysin θ=S,
×1×ysin θ=S,那么S△OA2B2=
 ×2×2ysin θ=4S,
×2×2ysin θ=4S,S△OA3B3=4S+(4S-S)=7S,
…,
S△OAnBn=
 x·xysin θ=(3n-2)S,
x·xysin θ=(3n-2)S,∴
 ,
,∴
 ,∴x=
,∴x= .即an=
.即an= (n≥3).
(n≥3).经验证知an=
 (n∈N*).
(n∈N*).
练习册系列答案
相关题目

 中,已知
中,已知 ,
, ,记
,记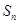 为数列
为数列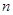 项和,则
项和,则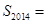 ( )
( )


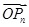 ·OPn+1的最小值;
·OPn+1的最小值;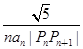 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值. ,求非零常数c.
,求非零常数c. +
+ +
+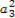 +…+
+…+ 等于( )
等于( ) (2n-1)2
(2n-1)2 的值是( )
的值是( )