题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,设圆
,设圆![]() 与圆
与圆![]() 的公共弦所在直线为
的公共弦所在直线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)若以坐标原点为中心,直线![]() 顺时针方向旋转
顺时针方向旋转![]() 后与圆
后与圆![]() 、圆
、圆![]() 分别在第一象限交于
分别在第一象限交于![]() 、
、![]() 两点,求
两点,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将圆![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;把两个圆的方程联立,即可得其公共弦所在直线方程,进而得其极坐标方程.
的极坐标方程化为直角坐标方程;把两个圆的方程联立,即可得其公共弦所在直线方程,进而得其极坐标方程.
(2)将圆![]() 的标准方程化为极坐标方程,将直线旋转后可得其角度,分别代入
的标准方程化为极坐标方程,将直线旋转后可得其角度,分别代入![]() 、
、![]() 的极坐标方程,即可由极坐标的几何意义求得
的极坐标方程,即可由极坐标的几何意义求得![]() .
.
(1)圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
则圆的普通方程为![]() ,
,
圆![]() 的极坐标方程为
的极坐标方程为![]() ,
,
等式两边同时乘以![]() 可得
可得![]() ,即
,即![]() ,化为直角坐标方程为
,化为直角坐标方程为![]() ,
,
圆![]() 与圆
与圆![]() 的公共弦所在直线为
的公共弦所在直线为![]() ,则
,则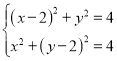 ,
,
化简可得![]() ,
,
所以直线![]() 的极坐标方程为
的极坐标方程为 ![]()
(2)以坐标原点为中心,直线![]() 顺时针方向旋转
顺时针方向旋转![]() 后与圆
后与圆![]() 、圆
、圆![]() 分别在第一象限交于
分别在第一象限交于![]() 、
、![]() 两点,
两点,
则直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
将圆![]() 的标准方程
的标准方程![]() 化为极坐标方程为
化为极坐标方程为![]() ,
,
设![]() ,
,![]()
则![]()
![]()

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | 18 | 30 |
非单车用户 | 38 | 32 | 70 |
合计 | 50 | 50 | 100 |
(1)从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
(2)将此样本的频率做为概率,从该市单车用户中随机抽取3人,记不小于40岁的单车用户的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: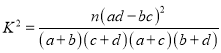 ,其中
,其中![]() )
)