题目内容
【题目】已知两个定点
，动点
满足
.设动点的轨迹为曲线
，直线
.
（1）求曲线的轨迹方程；
（2）若
与曲线交于不同的
两点，且
（
为坐标原点），求直线的斜率；
（3）若
， 
是直线上的动点，过作曲线的两条切线
，切点为
，探究：直线
是否过定点.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）设点P坐标为（x，y），运用两点的距离公式，化简整理，即可得到所求轨迹的方程；（2）由
，则点
到
边的距离为
，由点到线的距离公式得直线
的斜率；（3）由题意可知：O，Q，M，N四点共圆且在以OQ为直径的圆上，设
，则圆
的圆心为
运用直径式圆的方程，得直线
的方程为
，结合直线系方程，即可得到所求定点．
（1）设点
的坐标为
由
可得，
，
整理可得
所以曲线
的轨迹方程为.
（2）依题意，
，且，则点到边的距离为
即点
到直线
的距离
，解得
所以直线的斜率为.
（3）依题意，
，则
都在以
为直径的圆上
是直线
上的动点，设
则圆的圆心为，且经过坐标原点
即圆的方程为
，
又因为
在曲线
上
由
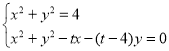，可得
即直线的方程为
由
且
可得，
解得
所以直线是过定点.
练习册系列答案
相关题目
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
为参数），在以原点为极点， 
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．
（1）求曲线
的普通方程和直线
的倾斜角；
（2）设点
，直线
和曲线
交于
两点，求
的值．
【题目】某种产品的广告费支出x与销售额y(单位：万元)之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）若广告费与销售额具有相关关系，求回归直线方程；
（2）在已有的五组数据中任意抽取两组，求两组数据其预测值与实际值之差的绝对值都不超过5的概率．
