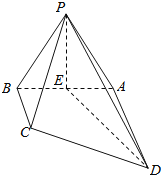
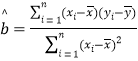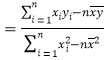题目内容
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
【答案】③④
【解析】
①根据![]() 与
与![]() 的关系即可判断;②当
的关系即可判断;②当![]() 时,
时,![]() ,对
,对![]() 求导可得
求导可得![]() ,设
,设![]() ,显然
,显然![]() 连续,利用零点存在性定理可得存在
连续,利用零点存在性定理可得存在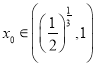 ,使得
,使得![]() ,即可判断
,即可判断![]() 时
时![]() 的单调性,进而判断②;由②可知当
的单调性,进而判断②;由②可知当![]() 时,
时,![]() 为
为![]() 的最小值,判断
的最小值,判断![]() 是否成立即可判断③;利用零点存在性定理即可判断④.
是否成立即可判断③;利用零点存在性定理即可判断④.
由题,![]() 的定义域为
的定义域为![]() ,
,
①![]() ,且
,且![]() ,所以
,所以![]() 不是奇函数,故①错误;
不是奇函数,故①错误;
②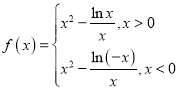 ,当
,当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,
,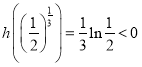 ,
,
所以存在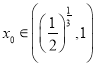 ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数,
是单调增函数,
所以②错误;
③由②可知,当![]() 时,
时,![]() 在
在![]() 上有最小值,且
上有最小值,且![]() ,
,
所以![]() ,
,
因为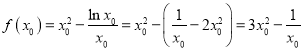 ,
,
由 ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,![]() 恒成立,故③正确;
恒成立,故③正确;
④当![]() 时,
时,![]() ,且
,且![]() ,
,![]() ,
,
所以![]() 在
在![]() 内有一个零点,故④正确.
内有一个零点,故④正确.
故答案为:③④

 课堂全解字词句段篇章系列答案
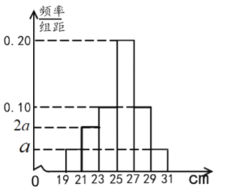
课堂全解字词句段篇章系列答案【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ),经统计,其高度均在区间
),经统计,其高度均在区间![]() 内,将其按
内,将其按![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
(1)求图中![]() 的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有
两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】某次考试,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:

根据以上信息,判断下列结论:
①根据此散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据此散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③甲同学数学考了80分,那么,他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为( ).
A.0B.3C.2D.1