题目内容
【题目】已知函数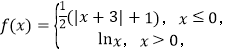
若存在实数
，满足
，则
的最大值是____．
【答案】
.
【解析】分析: 根据函数f（x）图象判断a，b，c关系即范围，用c表示出af（a）+bf（b）+cf（c），根据函数单调性求出最大值．
详解: 作出f（x）的函数图象如图所示：
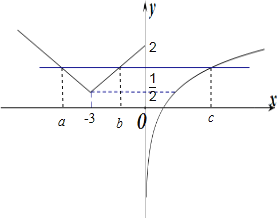
∵存在实数a＜b＜c，满足f（a）=f（b）=f（c），
∴a+b=﹣6，
∴af（a）+bf（b）+cf（c）=（a+b+c）f（c）=（c﹣6）lnc，
由函数图象可知：
＜c＜e2，
设g（c）=（c﹣6）lnc，则
=lnc+1﹣
，
显然在（，e2]上单调递增，
∵
=2﹣
＜0，
=3﹣
＞0，
∴在（，e2]上存在唯一一个零点，不妨设为c0，
在g（c）在（，c0）上单调递减，在（c0，e2]上单调递增，
又g（）=
（﹣6）＜0，g（e2）=2（e2﹣6）＞0，
∴g（c）的最大值为g（e2）=2e2﹣12．
故答案为：2e2﹣12
点睛: （1）本题有三个关键点,其一是能够很熟练准确地画出函数的图像；其二是从图像里能发现a+b=-6, ＜c＜e2；其三是能够想到构造函数g（c）=（c﹣6）lnc，利用导数求函数的最大值.（2）本题要求函数的图像和性质掌握的比较好，属于中档题.
名校课堂系列答案
【题目】某次考试，班主任从全班同学中随机抽取一个容量为8的样本，他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:
根据以上信息，判断下列结论:
①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为（ ）.
A.0B.3C.2D.1
