题目内容
已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将三角形AED折起，使DB=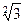
，
如图，O，H分别为AE、AB中点．
（Ⅰ）求证：直线OH//面BDE；
（Ⅱ）求证：面ADE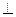
面ABCE；
（Ⅲ）求二面角O-DH-E的余弦值．
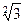，如图，O，H分别为AE、AB中点．
（Ⅰ）求证：直线OH//面BDE；
（Ⅱ）求证：面ADE
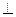面ABCE； （Ⅲ）求二面角O-DH-E的余弦值．略
练习册系列答案
相关题目
题目内容
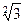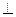，面ABCE； （Ⅲ）求二面角O-DH-E的余弦值．
是棱
的中点，
；
与平面
所成角大小（用反三角函数表示）．
如图，直三棱柱A1B1C1-ABC中，C1C=CB=CA=2，AC⊥CB．D、E分别为棱C1C、B1C1的中点． 
的球面上有
三点，
，
，
两点的球面距离为
，则球心到平面
的距离为_______________.
，则过A、B的平面中，与球心的最大距离是 
，则它的外接球半径R与内切球半径
之比为（ ）
中，
，AB=2，点E在棱AB上移动．
；
的距离；
的大小为
．
的球面上的三点，
，O为球心，则直线OA与截面ABC所成的角是（ ）
B．
C．
