题目内容
(本小题满分13分)
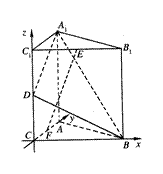
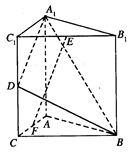 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求A1B与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点. (Ⅰ)求A1B与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
 ,
,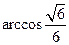 ,线段AC的中点F
,线段AC的中点F解:(Ⅰ)连接A1C.∵A1B1C1-ABC为直三棱柱,∴CC1⊥底面ABC,∴CC1⊥BC.
∵AC⊥CB,∴BC⊥平面A1C1CA.
∴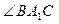 为
为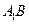 与平面A1C1CA所成角,
与平面A1C1CA所成角,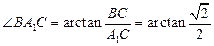 .
.
∴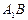 与平面A1C1CA所成角为
与平面A1C1CA所成角为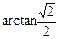 .
.
(Ⅱ)分别延长AC,A1D交于G. 过C作CM⊥A1G于M,连结BM,
∵BC⊥平面ACC1A1,∴CM为BM在平面A1C1CA内的射影,
∴BM⊥A1G,∴∠CMB为二面角B—A1D—A的平面角,
平面A1C1CA中,C1C=CA=2,D为C1C的中点,
∴CG=2,DC="1" 在直角三角形CDG中,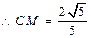 ,
,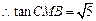 .
.
即二面角B—A1D—A的大小为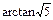 .
.
(Ⅲ)取线段AC的中点F,则EF⊥平面A1BD.
证明如下:
∵A1B1C1—ABC为直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA内的射影为C1F,当F为AC的中点时,
C1F⊥A1D,∴EF⊥A1D.
同理可证EF⊥BD,∴EF⊥平面A1BD.
解法二:
(Ⅰ)同解法一
(Ⅱ)∵A1B1C1—ABC为直三棱柱,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点.
建立如图所示的坐标系得:
C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2).
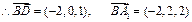 ,设平面A1BD的法向量为
,设平面A1BD的法向量为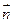
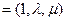 ,
,
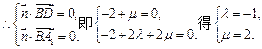
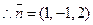 .
.
平面ACC1A1的法向量为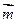 =(1,0,0),
=(1,0,0),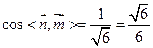 .
.
即二面角B—A1D—A的大小为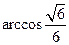 .
.
(Ⅲ)F为AC上的点,故可设其坐标为(0,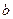 ,0),∴
,0),∴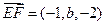 .
.
由(Ⅱ)知 是平面A1BD的一个法向量,
是平面A1BD的一个法向量,
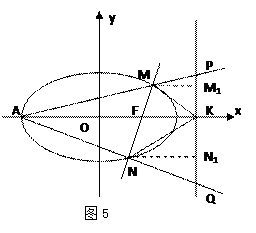 欲使EF⊥平面A1BD,当且仅当
欲使EF⊥平面A1BD,当且仅当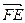 //
//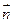 .
.
∴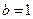 ,∴当F为AC的中点时,EF⊥平面A1BD.
,∴当F为AC的中点时,EF⊥平面A1BD.

∵AC⊥CB,∴BC⊥平面A1C1CA.
∴
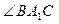 为
为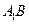 与平面A1C1CA所成角,
与平面A1C1CA所成角,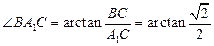 .
.∴
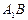 与平面A1C1CA所成角为
与平面A1C1CA所成角为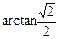 .
. (Ⅱ)分别延长AC,A1D交于G. 过C作CM⊥A1G于M,连结BM,
∵BC⊥平面ACC1A1,∴CM为BM在平面A1C1CA内的射影,
∴BM⊥A1G,∴∠CMB为二面角B—A1D—A的平面角,
平面A1C1CA中,C1C=CA=2,D为C1C的中点,
∴CG=2,DC="1" 在直角三角形CDG中,
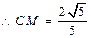 ,
,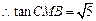 .
. 即二面角B—A1D—A的大小为
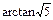 .
. (Ⅲ)取线段AC的中点F,则EF⊥平面A1BD.
证明如下:
∵A1B1C1—ABC为直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA内的射影为C1F,当F为AC的中点时,
C1F⊥A1D,∴EF⊥A1D.
同理可证EF⊥BD,∴EF⊥平面A1BD.
解法二:
(Ⅰ)同解法一
(Ⅱ)∵A1B1C1—ABC为直三棱柱,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点.
建立如图所示的坐标系得:
C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2).
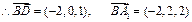 ,设平面A1BD的法向量为
,设平面A1BD的法向量为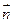
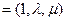 ,
,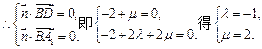
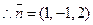 .
.平面ACC1A1的法向量为
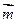 =(1,0,0),
=(1,0,0),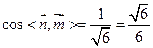 .
.即二面角B—A1D—A的大小为
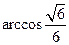 .
.(Ⅲ)F为AC上的点,故可设其坐标为(0,
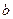 ,0),∴
,0),∴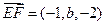 .
.由(Ⅱ)知
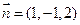 是平面A1BD的一个法向量,
是平面A1BD的一个法向量, 欲使EF⊥平面A1BD,当且仅当
欲使EF⊥平面A1BD,当且仅当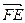 //
//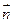 .
. ∴
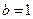 ,∴当F为AC的中点时,EF⊥平面A1BD.
,∴当F为AC的中点时,EF⊥平面A1BD.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
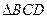 与
与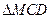 都是边长为2的正三角形,
都是边长为2的正三角形,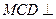 平面
平面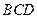 ,
,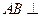 平面
平面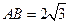 .
.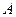 到平面
到平面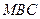 的距离;
的距离;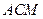 与平面
与平面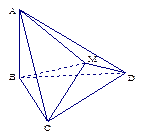
 中,
中,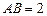 ,
, ,
,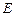 是
是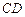 的中点,以
的中点,以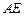 为折痕将
为折痕将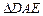 向上折起,使
向上折起,使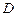 为
为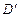 ,且平面
,且平面 平面
平面
 ;
;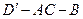 的大小;
的大小;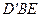 的距离.
的距离. 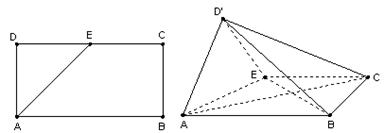
 圈上有甲、已两地,甲地位于东径
圈上有甲、已两地,甲地位于东径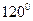 ,乙地位于西径
,乙地位于西径 ,则地球(半径为R)表面上甲、乙两地的最短距离为_________
,则地球(半径为R)表面上甲、乙两地的最短距离为_________ 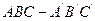 ,
,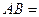
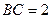 ,
,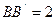 ,N、M分别是
,N、M分别是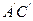 、
、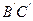 的中点
的中点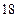
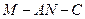 的余弦值
的余弦值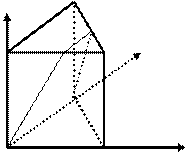
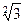 ,
, 面ABCE;
面ABCE;  (Ⅲ)求二面角O-DH-E的余弦值.
(Ⅲ)求二面角O-DH-E的余弦值.