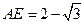题目内容
(本小题满分13分)
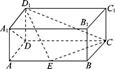
如图,在长方体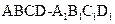 中,
中,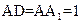 ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.
(Ⅰ)证明: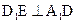 ;
;
(Ⅱ)当E为AB的中点时,求点A到面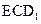 的距离;
的距离;
(Ⅲ)AE等于何值时,二面角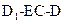 的大小为
的大小为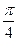 .
.

如图,在长方体
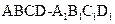 中,
中,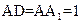 ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.(Ⅰ)证明:
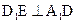 ;
;(Ⅱ)当E为AB的中点时,求点A到面
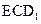 的距离;
的距离;(Ⅲ)AE等于何值时,二面角
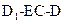 的大小为
的大小为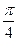 .
.(1)略;(2)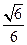 ;(3)
;(3)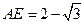
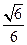 ;(3)
;(3)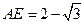
略

练习册系列答案
相关题目
题目内容

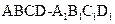 中,
中,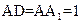 ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.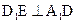 ;
;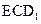 的距离;
的距离;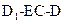 的大小为
的大小为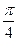 .
.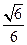 ;(3)
;(3)