题目内容
12.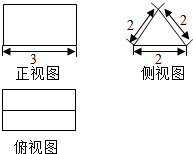 已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
分析 根据几何体的三视图,得出该几何体是平放的直三棱柱,结合图中数据求出它的体积与表面积.
解答 解:根据几何体的三视图,得:
该几何体是平放的直三棱柱,
且三棱柱的底面是边长为2的正三角形,棱柱的高为3;
所以,该三棱柱的体积是:
V=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×22×3=3$\sqrt{3}$cm2,
它的表面积是:
S=2×$\frac{\sqrt{3}}{4}$×22+3×2×3=18+2$\sqrt{3}$cm3.
故答案为:3$\sqrt{3}$,18+2$\sqrt{3}$.
点评 本题考查了利用空间几何体的三视图求体积与表面积的应用问题,是基础题目.

练习册系列答案
相关题目
20.在x轴、y轴上截距分别是2、-3的直线的方程为( )
| A. | 3x-2y+6=0 | B. | 3x+2y+1=0 | C. | 3x-2y-6=0 | D. | 3x-2y+1=0 |
7.在圆x2+y2=4上,与直线4x-4y+21=0的距离最小的点的坐标为( )
| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,-$\sqrt{2}$) |
17.在等差数列{an}中,Sn为其前n项和,若a3=8,则S5=( )
| A. | 16 | B. | 24 | C. | 32 | D. | 40 |
1.△ABC中,已知a,b,c分别为角A,B,C的对边且∠A=60°,若${S_{△ABC}}=\frac{{3\sqrt{3}}}{2}$,且2sinB=3sinC,则△ABC的周长等于( )
| A. | $5+\sqrt{7}$ | B. | 12 | C. | 10+$\sqrt{7}$ | D. | 5+$2\sqrt{7}$ |
2.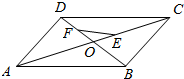 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )| A. | $\overrightarrow{FE}$=-$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | B. | $\overrightarrow{FE}$=$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | C. | $\overrightarrow{FE}$=$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ | D. | $\overrightarrow{FE}$=-$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ |