题目内容
1.△ABC中,已知a,b,c分别为角A,B,C的对边且∠A=60°,若${S_{△ABC}}=\frac{{3\sqrt{3}}}{2}$,且2sinB=3sinC,则△ABC的周长等于( )| A. | $5+\sqrt{7}$ | B. | 12 | C. | 10+$\sqrt{7}$ | D. | 5+$2\sqrt{7}$ |
分析 由条件利用正弦定理可得2b=3c,再由S△ABC=$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$bc•sinA,求得bc,从而求得b和c的值.再由余弦定理求得a,从而得到三角形的周长.
解答 解:在△ABC中,角A=60°,
∵2sinB=3sinC,故由正弦定理可得 2b=3c,
再由S△ABC=$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$bc•sinA,可得 bc=6,
∴b=3,c=2.
再由余弦定理可得 a2=b2+c2-2bc•cosA=19,
解得:a=$\sqrt{7}$.
故三角形的周长a+b+c=5+$\sqrt{7}$,
故选:A.
点评 本题主要考查正弦定理和余弦定理在解三角形中的应用,考查了计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若函数f(x)=(2m-1)x${\;}^{{m}^{2}-2}$是幂函数,则 f(-2)=( )
| A. | -1 | B. | -2 | C. | 1 | D. | -$\frac{1}{2}$ |
11.已知$\overrightarrow a=(5,6),\overrightarrow b=(sinα,cosα)$,且$\overrightarrow a∥\overrightarrow b$,则tanα=( )
| A. | $-\frac{5}{6}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
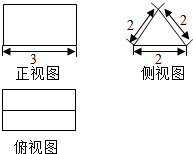 已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.