题目内容
5.欧阳修的《卖油翁》中写道:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是半径为3cm的圆,中间有一正方形的钱孔,随机向铜钱上滴三滴油(油滴的大小忽略不计),至少有一滴油落入孔中的概率是$\frac{7}{8}$,则正方形钱孔的边长是$\frac{3}{2}\sqrt{2π}$.分析 设随机向铜钱上滴一滴油(油滴的大小忽略不计),油落入孔中的概率是P,结合已知可得P=$\frac{1}{2}$,设正方形钱孔的边长是a,代入几何概型概率计算公式,可得答案.
解答 解:∵设随机向铜钱上滴一滴油(油滴的大小忽略不计),油落入孔中的概率是P,
则随机向铜钱上滴三滴油(油滴的大小忽略不计),至少有一滴油落入孔中的概率是$\frac{7}{8}$,
则随机向铜钱上滴三滴油(油滴的大小忽略不计),三滴均落在孔外的概率是1-$\frac{7}{8}$=$\frac{1}{8}$,
即(1-P)3=$\frac{1}{8}$,
解得:P=$\frac{1}{2}$,
设正方形钱孔的边长是a,则$\frac{{a}^{2}}{π•{3}^{2}}$=$\frac{1}{2}$,
解得:a=$\frac{3}{2}\sqrt{2π}$,
故答案为:$\frac{3}{2}\sqrt{2π}$
点评 本题考查的知识点是几何概型,对立事件概率减法公式,相互独立事件概率乘法公式,难度中档.

练习册系列答案
相关题目
16.n为整数,化简$\frac{sin(nπ-α)}{cos(nπ-α)}$所得结果是( )
| A. | tannα | B. | -tannα | C. | tanα | D. | -tanα |
20.p:x2=3x-2是q:x=$\sqrt{3x-2}$的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.已知定义在R上的奇函数f(x)满足f(x-1)=f(x+1),当x∈(0,1]时,f(x)=x+3,则f(-$\frac{5}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | $\frac{7}{2}$ |
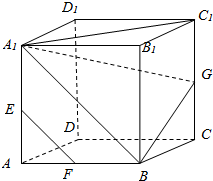 在正方体AC1中.
在正方体AC1中.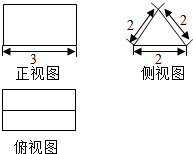 已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.