题目内容
4.已知椭圆E的中心在坐标原点,离心率为$\frac{1}{2}$,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=6.分析 利用椭圆的离心率以及抛物线的焦点坐标,求出椭圆的半长轴,然后求解抛物线的准线方程,求出A,B坐标,则|AB|可求.
解答 解:椭圆E的中心在坐标原点,离心率为$\frac{1}{2}$,E的右焦点(c,0)与抛物线C:y2=8x的焦点(2,0)重合,
可得c=2,a=4,b2=12,椭圆的标准方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,
抛物线的准线方程为:x=-2,
联立$\left\{\begin{array}{l}{x=-2}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,解得y=±3,
∴A(-2,3),B(-2,-3).
则|AB|=3-(-3)=6.
故答案为:6.
点评 本题考查抛物线以及椭圆的简单性质的应用,考查计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知定义在R上的奇函数f(x)满足f(x-1)=f(x+1),当x∈(0,1]时,f(x)=x+3,则f(-$\frac{5}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | $\frac{7}{2}$ |
19.函数f(x)=$\frac{1}{\sqrt{1-{e}^{x}}}$的定义域是( )
| A. | (0,+∞) | B. | (-∞,0] | C. | (-∞,0) | D. | (-∞,+∞) |
 已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.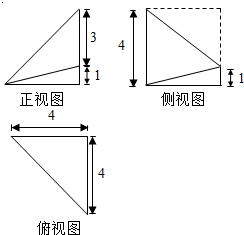 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.