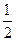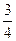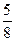题目内容
(本题满分10分)
数列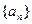 满足
满足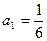 ,前n项和
,前n项和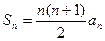 .
.
(Ⅰ)写出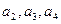 ;
;
(Ⅱ)猜出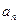 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
数列
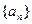 满足
满足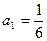 ,前n项和
,前n项和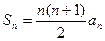 .
.(Ⅰ)写出
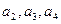 ;
;(Ⅱ)猜出
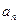 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.(1)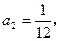
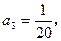
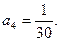 (2)
(2)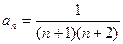
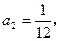
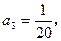
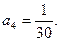 (2)
(2)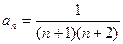
(Ⅰ)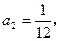
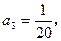
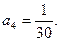
(Ⅱ)猜想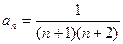 ,下面用数学归纳法给出证明.
,下面用数学归纳法给出证明.
①当n=1时,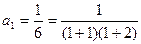 结论成立.
结论成立.
②假设当n=k时,结论成立,即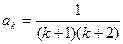 ,
,
那么当n=k+1时,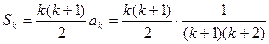 =
=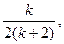
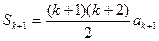
即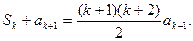
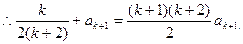
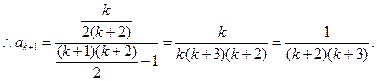
∴当n=k+1时结论成立.
由①②可知,对一切 ,都有
,都有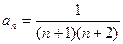 成立
成立
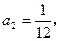
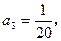
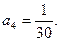
(Ⅱ)猜想
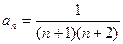 ,下面用数学归纳法给出证明.
,下面用数学归纳法给出证明.①当n=1时,
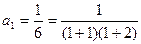 结论成立.
结论成立.②假设当n=k时,结论成立,即
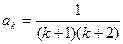 ,
,那么当n=k+1时,
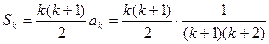 =
=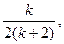
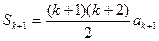
即
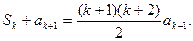
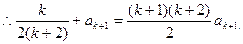
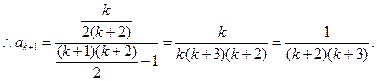
∴当n=k+1时结论成立.
由①②可知,对一切
 ,都有
,都有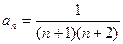 成立
成立
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 的前
的前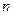 项和为
项和为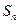 ,
,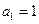 ,
,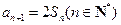 .
.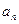 ;(Ⅱ)求数列
;(Ⅱ)求数列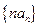 的前
的前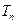 .
.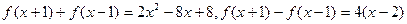 ,且
,且 ,
,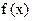 是一个递增的等差数列
是一个递增的等差数列 的前三项,
的前三项, 的值
的值 满足:
满足: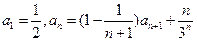
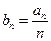 ,求数列
,求数列 的通项公式;
的通项公式;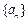 的前n项和为
的前n项和为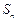 ,已知
,已知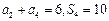 .
.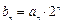
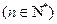 ,求数列
,求数列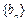 的前n项和
的前n项和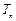 .
.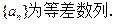 且
且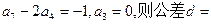 ( )
( ) ,第二组含两个数
,第二组含两个数 ,第三组含三个数
,第三组含三个数 ,第四组含四个数
,第四组含四个数 ,┅,现观察猜想每组内各数之和与其组的编号数
,┅,现观察猜想每组内各数之和与其组的编号数 的关系为( )
的关系为( )





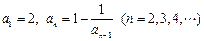 ,则
,则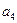 = ;若有一个形如
= ;若有一个形如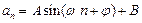 的通项公式,其中A, B,
的通项公式,其中A, B, 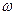 ,
,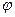 均为实数,且
均为实数,且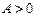 ,
,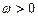 ,
,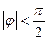 ,则此通项公式可以为
,则此通项公式可以为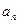 = (写出一个即可)
= (写出一个即可)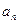 }中的首项
}中的首项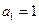 ,且满足
,且满足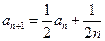 ,则此数列的第3项是( )
,则此数列的第3项是( )