题目内容
已知点P(2,0)及圆C:x2+y2-6x+4y+4=0.
(1)若圆C与圆x2+y2+2x-2y+m=0外切,求m的值;
(2)设过点P的直线l1与圆C交于M、N两点,当|MN|=4时,求以线段MN为直径的圆Q的方程.
(1)若圆C与圆x2+y2+2x-2y+m=0外切,求m的值;
(2)设过点P的直线l1与圆C交于M、N两点,当|MN|=4时,求以线段MN为直径的圆Q的方程.
(1)圆C:x2+y2-6x+4y+4=0,化为(x-3)2+(y+2)2=9,圆心C(3,-2),半径R=3.
圆Ex2+y2+2x-2y+m=0化为(x+1)2+(y-1)2=2-m,圆心E(-1,1),半径r=
.
∵此两圆相外切,∴|CE|=R+r,
∴
=3+
,化为
=2,解得m=-2.
∴m的值为-2.
(2)设M(x1,y1),N(x2,y2).
①当直线l1的斜率存在时,设直线l1的方程为y=k(x-2).
由圆C:x2+y2-6x+4y+4=0,圆心C(3,-2),半径R=3.
∴圆心C到直线l1的距离d=
.
∵|MN|=4,∴d2+(
)2=R2,
∴(
)2+22=32,解得k=
.
联立
,化为5x2-20x+4=0,
∴x1+x2=4,∴
=2.
∴
=
(2-2)=0,∴以线段MN为直径的圆的方程为(x-2)2+y2=4.
②当直线l1的斜率不存在时,弦长=2
=4
不符合题意,应舍去.
故以线段MN为直径的圆的方程为(x-2)2+y2=4.
圆Ex2+y2+2x-2y+m=0化为(x+1)2+(y-1)2=2-m,圆心E(-1,1),半径r=
| 2-m |
∵此两圆相外切,∴|CE|=R+r,
∴
| (-1-3)2+(1+2)2 |
| 2-m |
| 2-m |
∴m的值为-2.
(2)设M(x1,y1),N(x2,y2).
①当直线l1的斜率存在时,设直线l1的方程为y=k(x-2).
由圆C:x2+y2-6x+4y+4=0,圆心C(3,-2),半径R=3.
∴圆心C到直线l1的距离d=
| |3k+2-2k| | ||
|
∵|MN|=4,∴d2+(
| |MN| |
| 2 |
∴(
| k+2 | ||
|
| 1 |
| 2 |
联立
|
∴x1+x2=4,∴
| x1+x2 |
| 2 |
∴
| y1+y2 |
| 2 |
| 1 |
| 2 |
②当直线l1的斜率不存在时,弦长=2
| R2-12 |
| 2 |
故以线段MN为直径的圆的方程为(x-2)2+y2=4.

练习册系列答案
相关题目
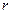 >0,两圆
>0,两圆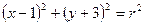 与
与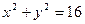 可能( )
可能( )