题目内容
若圆C1:x2+y2+2ax+a2-4=0(a∈R)与圆C2:x2+y2-2by+b2-1=0(b∈R)外切,则a+b的最大值为______.
圆C1:x2+y2+2ax+a2-4=0(a∈R)的标准方程为(x+a)2+y2=4;
圆C2:x2+y2-2by+b2-1=0(b∈R)的标准方程为x2+(y-b)2=1
∵两圆外切
∴a2+b2=9
∵a2+b2≥2ab
∴2(a2+b2)≥(a+b)2
∴18≥(a+b)2
∴-3
≤a+b≤3
∴a+b的最大值为3
故答案为:3
圆C2:x2+y2-2by+b2-1=0(b∈R)的标准方程为x2+(y-b)2=1
∵两圆外切
∴a2+b2=9
∵a2+b2≥2ab
∴2(a2+b2)≥(a+b)2
∴18≥(a+b)2
∴-3
| 2 |
| 2 |
∴a+b的最大值为3
| 2 |
故答案为:3
| 2 |

练习册系列答案
相关题目
 ;
; .
.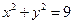 和
和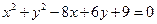 的位置关系是( )
的位置关系是( )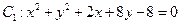 ,圆
,圆 ,经判断这两个圆的位置关系是
,经判断这两个圆的位置关系是