题目内容
6.已知单调递减的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4是等差中项.(1)求数列{an}的通项公式;
(2)若bn=log2an,求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Sn.
分析 根据题意得出方程组:$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{2}+{a}_{1}{q}^{3}=28①}\\{a(q+{q}^{3})=2({a}_{1}{q}^{2}+2)②}\end{array}\right.$求解得出q=$\frac{1}{2}$或q=2,单调递减得出:q=$\frac{1}{2}$,根据通项公式求解即可.
(2)根据对数运算得出bn=log2an=6-n,运用裂项法$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(6-n)(5-n)}$=$\frac{1}{5-n}$$-\frac{1}{6-n}$
求解得出Sn即可.
解答 解:(1)设等比数列{an}的首项为a1,公比为q,则
$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{2}+{a}_{1}{q}^{3}=28①}\\{a(q+{q}^{3})=2({a}_{1}{q}^{2}+2)②}\end{array}\right.$
由②×7-①得:2q2-5q+2=0
所以q=$\frac{1}{2}$或q=2
因为等比数列{an}为递减数列,
所以q=$\frac{1}{2}$,a1=32,即an=32×($\frac{1}{2}$)n-1=26-n
(2)bn=log2an=6-n,
因为$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(6-n)(5-n)}$=$\frac{1}{5-n}$$-\frac{1}{6-n}$
所以Sn=$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{3}$$-\frac{1}{4}$$+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{6-n}$$-\frac{1}{7-n}$$+\frac{1}{5-n}$$-\frac{1}{6-n}$=$\frac{1}{5-n}$$-\frac{1}{5}$=$\frac{n}{25-5n}$(n<5).
点评 本题综合考查了等比数列的性质,公式,方程组的方法求解,解题时要注意等比数列和等差数列的性质的灵活运用,裂项法求解数列的和,属于中档题.

 2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | 0~50 | 51~200 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
(1)求直方图中x的值;
(2)计算一年中空气质量为良和轻微污染的总天数;
(3)求该城市一年中每天空气质量不为良且不为轻微污染的概率.
| A. | f(x)=x2 | B. | f(x)=-log2|x| | C. | f(x)=3|x| | D. | f(x)=sinx |
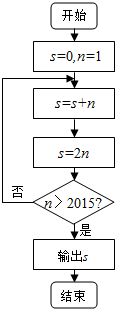
| A. | 210-1 | B. | 211-1 | C. | 21007-1 | D. | 21024-1 |
