题目内容
4.已知P为椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点,如果存在过点M(x0,0)(x0>0)的直线交椭圆于A、B两点,使得S△AOB=2S△AOP,则x0的取值范围是( )| A. | (1,$\sqrt{3}$] | B. | [$\sqrt{3}$,2) | C. | (1,2) | D. | (1,+∞) |
分析 如图所示,设直线AB的方程为:ty=x-x0,A(x1,y1),B(x2,y2),与椭圆方程联立化为(4+t2)y2-2tx0y+${x}_{0}^{2}$-4=0.△>0.由于S△AOP=$\frac{1}{2}×|OP|•{y}_{1}$=y1,S△AOB=$\frac{1}{2}{x}_{0}|{y}_{1}-{y}_{2}|$.S△AOB=2S△AOP,可得2y1=$\frac{1}{2}{x}_{0}|{y}_{1}-{y}_{2}|$.再利用根与系数的关系可得:t2=$\frac{{x}_{0}^{4}-4{x}_{0}^{3}+16{x}_{0}-16}{4(1-{x}_{0})}$.令m=x0,f(m)=m4-4m3+16m-16,(m∈(0,2)),利用导数研究其单调性即可得出.
解答 解:如图所示,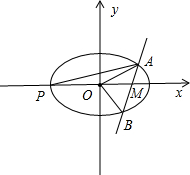
设直线AB的方程为:ty=x-x0,A(x1,y1),B(x2,y2),(y1>y2,y1>0).
联立$\left\{\begin{array}{l}{ty=x-{x}_{0}}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
化为(4+t2)y2+2tx0y+${x}_{0}^{2}$-4=0.
∴△=$4{t}^{2}{x}_{0}^{2}$-4$(4+{t}^{2})({x}_{0}^{2}-4)$>0,
∴y1+y2=-$\frac{2t{x}_{0}}{4+{t}^{2}}$,①
y1y2=$\frac{{x}_{0}^{2}-4}{4+{t}^{2}}$,②
S△AOP=$\frac{1}{2}×|OP|•{y}_{1}$=y1,S△AOB=$\frac{1}{2}{x}_{0}|{y}_{1}-{y}_{2}|$.
∵S△AOB=2S△AOP,
∴2y1=$\frac{1}{2}{x}_{0}|{y}_{1}-{y}_{2}|$.
化为${y}_{2}=(1-\frac{4}{{x}_{0}}){y}_{1}$,代入①可得:y1=$\frac{2t{x}_{0}^{2}}{(2{x}_{0}-4)(4+{t}^{2})}$,
∴y2=$\frac{2t{x}_{0}({x}_{0}-4)}{(2{x}_{0}-4)(4+{t}^{2})}$,
∴$\frac{2t{x}_{0}^{2}}{(2{x}_{0}-4)(4+{t}^{2})}$•$\frac{2t{x}_{0}({x}_{0}-4)}{(2{x}_{0}-4)(4+{t}^{2})}$=$\frac{{x}_{0}^{2}-4}{4+{t}^{2}}$,
化为t2=$\frac{{x}_{0}^{4}-4{x}_{0}^{3}+16{x}_{0}-16}{4(1-{x}_{0})}$.(*)
令m=x0,f(m)=m4-4m3+16m-16,(m∈(0,2)),
f′(m)=4m3-12m2+16=4(m-2)2(m+1),
∴函数f(m)在m∈(0,2)单调递增,
又f(0)=-16,f(1)=-3,f(2)=0,
因此要使(*)有解,则1<m<2,即x0∈(1,2).
故选:C.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、三角形面积计算公式、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | (-1,2) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
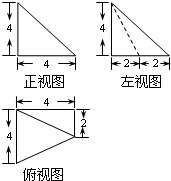
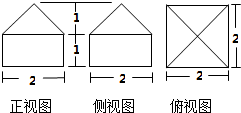 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.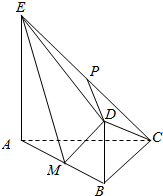 如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.
如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.