题目内容
6.在区间[-π,π]内随机取两个数分别记为m,n,则使得函数f(x)=$\frac{1}{3}$x3+mx2-(n2-π)x+1有极值点的概率为$\frac{3}{4}$.分析 根据f(x)有极值,得到f'(x)=0有两个不同的根,求出a、b的关系式,利用几何概型的概率公式即可的得到结论
解答 解:在区间[-π,π]内随机取两个数分别记为m,n,则使得函数f(x)=$\frac{1}{3}$x3+mx2-(n2-π)x+1有极值点
则f′(x)=x2+2mx-(n2-π)=0有两个不同的根,
即判别式△=4m2+4(n2-π)>0,即m2+n2>π对应区域的面积为4π2-π2.
如图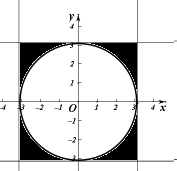
∴由几何概型的概率公式可得对应的概率P=$\frac{4{π}^{2}-{π}^{2}}{4{π}^{2}}=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题主要考查几何概型的概率的计算,利用函数取得极值的条件求出对应a的取值范围是解决本题的关键

练习册系列答案
相关题目
16.若函数f(x)在R上可导,且f(x)>f′(x),则当a>b时,下列不等式成立的是( )
| A. | eaf(a)>ebf(b) | B. | ebf(a)>eaf(b) | C. | ebf(b)>eaf(a) | D. | eaf(b)>ebf(a) |
17.执行如图所示的程序框图,如果输入的x∈R,则输出的h(x)的最小值是( )


| A. | $\frac{3}{4}$ | B. | 3 | C. | 4 | D. | 7 |
11.在△ABC中,内角A,B,C所对应的边分别为a,b,c,若bsinA-$\sqrt{3}$acosB=0,且b2=ac,则$\frac{b}{a+c}$的值为
( )
( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
18.已知变量x与y线性相关,数据如表:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 6 | 7 |
| A. | (1,3) | B. | (2,6) | C. | (3,7) | D. | (1.5,4) |
15.已知f(x)=|x-2|-1,若直线y=m与函数y=f[f(x)]的图象有四个不同的交点,则实数m的取值范围是( )
| A. | (-1,2) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
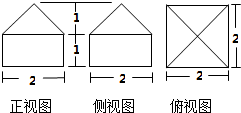 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.