题目内容
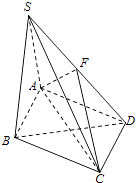
【题目】如图，矩形ABCD中，AB=2BC=4，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中： ①|BM|是定值；
②点M在圆上运动；
③一定存在某个位置，使DE⊥A1C；
④一定存在某个位置，使MB∥平面A1DE．
其中正确的命题是（ ）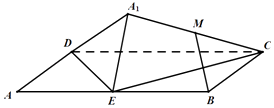
A.①②③
B.①②④
C.①③④
D.②③④
【答案】B
【解析】解：取CD中点F，连接MF，BF，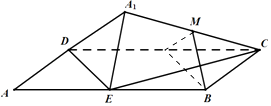
则MF∥DA1 ， BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故④正确
由∠A1DE=∠MFB，MF= 
A1D=定值，FB=DE=定值，
由余弦定理可得MB2=MF2+FB2﹣2MFFBcos∠MFB，所以MB是定值，故①正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故②正确，
∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，
∴存在某个位置，使DE⊥A1C不正确，故③不正确．
故选：B．
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案，需要熟知两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．
练习册系列答案
相关题目
