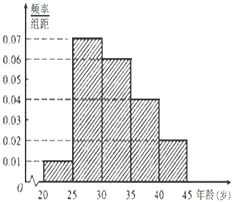
题目内容
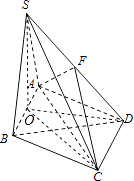
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 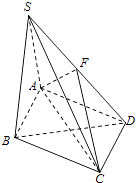
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
【答案】
(1)解:由题意,三棱锥S﹣FAC的体积=三棱锥S﹣DAC的体积的一半.
取AB的中点O,连接SO,则SO⊥底面ABCD,SO= ![]() ,
,
∵S△DAC= ![]() =
= ![]() ,
,
∴三棱锥S﹣FAC的体积= ![]() =
= ![]()
(2)解:连接OD,OC,则OC=OD= ![]() ,∴SC=SD=3,
,∴SC=SD=3,
△SAD中,SA=AD=2,F为SD的中点,∴AF= ![]() =
= ![]() .
.
△SCD中,SC=SD=3,CD=2,∴9+4CF2=2(9+4),∴CF= ![]() ,
,
△FAC中,cos∠AFC= 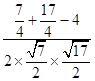 =
= ![]() ,
,
∴sin∠AFC= ![]() ,
,
∴S△AFC= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]()
设D到平面AFC的距离为h,则 ![]() ,∴h=
,∴h= ![]() ,
,
∴直线BD与平面FAC所成角的正弦值 ![]() ÷
÷ ![]() =
= ![]()
【解析】(1)由题意,三棱锥S﹣FAC的体积=三棱锥S﹣DAC的体积的一半,取AB的中点O,连接SA,利用体积公式求三棱锥S﹣FAC的体积;(2)求出D到平面AFC的距离,即可求直线BD与平面FAC所成角的正弦值.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则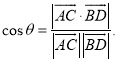 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目